wyznacz prostą AC Frajvald: Mógłby ktoś pomoc z takim zadaniem? W trójkącie równobocznym ABC dane są współrzędne wierzchołków A = (2,1) oraz B = (8,4) . Wyznacz równanie prostej zawierającej bok AC tego trójkąta. Próbowałem ze wzoru na kąt ostry pomiędzy prostymi i mi nie wyszło,pózniej wyznaczyłem prostą CS i odcinek |AB|=3√5 i z tego wyznaczyć punkt C ale wciąż nie chce mi wyjść wynik. Odp to y = (8+5√3) x −10√3 −15 lub y = (8−5√3) x +10√3 −15

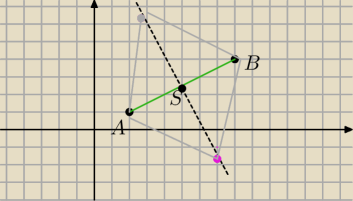
a7: liczymy prostą AB liczymy środek odcinka AB, liczymy prostą prostopadłą do prostej AB przechodzącą przez punkt S liczymy punkt C na prostej obliczonej, wyznaczamy go z długości odcinka i wyjdą dwie opcje szukane

Frajvald: Pisałem na górze, że robiłem w ten sposób i mi nie wyszlo ale skoro piszesz ze to dobry sposob to znaczy ze po prostu mam gdzies błąd w obliczeniach

a7: no a potem wyznaczamy jeszcze te szukane proste

a7: nie widzę byś wyznaczył prostą AB? jakie wspołrzędne ma punkt S

a7: podaj dane to policzę dalej

a7: te dane

a7: jakie jest równanie prostej prostopadłej przechodzącej przez punkt S

a7: ?

Frajvald: S=(5:2,5) prosta CS: y=−2x+12,5

a7: a prosta AB?

Frajvald:

	3√15
długość CS wyszła mi :
	2

Frajvald:

	1
AB: y=		x
	2

a7: C(x_c,−2x_c+12,5) |BC|=3√5 B=8,4 A=2,1 x_c=x (x−8)²+(−2x+12,5−4)²=45 x=(5−6√3)/4 lub x=(5+6√3)/4 y=..... y=...............

Frajvald: Bardzo dziękuje za pomoc

a7: wyszło?

Frajvald:

	10−3√3		10+3√3
Niestety nie, przeliczyłem z BC i wyszło mi znowu x1=		i x2=		i z
	2		2

tego nie mogę wyznaczyć a

a7: to ja pokaże jak liczyłam i zobaczymy kto ma błąd ok?

a7: 5x²−50x+91,25=0

a7: 20x²−200x+365=0

Frajvald: Tak, też mi wychodziło to samo za każdym razem

a7: Δ=10800=60√3

	5−6√3		5+6√3
x=(50−60√3)/40=		lub x=(50+60√3)/40 =
	4		4

a7: poprawka √Δ=60√3

a7:

	6√3−5		−6√3−5
y1=		+12,5 y2=		+12,5
	2		2

a7: ok teraz liczę proste AC, tak?

Frajvald: Tak, a możesz pokazac jak wyliczasz AC? bo mi to wlasnie nie chce wyjsc,btw bardzo dziękuje za poswięcony czas i ja to obliczałem w ten sposób 5x²−50x+91,25=0 delta= 2500−1825 = 675=(15√3)²

	50−15√3		10−3√3
i x1=		=
	10		2

	50+15√3		10+3√3
i x2 =		=
	10		2

a7: no tak to u mnie błąd to jakie ygreki

a7: i policzę AC

Frajvald: y1 = 3√3+2,5 y2=−3√3+2,5

a7: a na pewno takie?

a7: ok

Frajvald: cóż z tych punktów x takie mi wyszły, ale chyba dam temu spokój albo mam jakiś minimalny błąd w obliczeniach albo są zle odpowiedzi

Frajvald: jeszcze raz bardzo dziekuje za poswiecony czas i pomoc

a7: niestety wychodzi mi też inny wynik

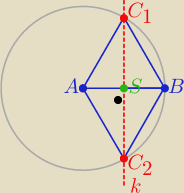
Eta: |AB|²=45 , S(5,5/2) a_AB=1/2 to prosta k : y=−2(x−5)+5/2 ⇒ k: y=−2x+25/2 Okrąg o środku A i promieniu r przecina prostą k w punktach C₁, C₂ to (x−2)²+(y−1)²=45 i k.. po uporządkowaniu otrzymujemy

	73
x2−10x+		=0 , Δ=27 ,
	4

	10−3√3		10+3√3
x=		v x=
	2		2

	6√3+5		5−6√3
y=		v y=
	2		2

C₁(...... , ..... ) C₂(......, .....) współczynniki kierunkowe prostych AC₁ i AC₂

	yC1−yA		2√3+1
a1=		= ......=		= ..... = 8+5√3
	xC1−xA		2−√3

	1−2√3
a2=		=....=8−5√3
	2+√3

Równania tych prostych: AC₁: y= (8+5√3(x−2)+1 , A_C2: y= (8−5√3)(x−2)+1 otrzymujemy: y=(8+5√3)x−10√3−15 lub y= (8−5√3)x+10√3−15 ========================================

Eta: Wielka szkoda,że teraz nie ma w programie równań obrotu dookoła punktu o kąt α W tym zadaniu obrót o kąt 60^o lub o kąt −60^o i byłoby łatwiej dojść do celu

Frajvald: O dziękuje bardzo za rozwiązanie,czyli jednak nie było błędu w zadaniu, dzięki twojemu rozwiązaniu w koncu u siebie zauważyłem błąd

Eta: Na zdrowie

fgrt: