Czworokąt wpisany w okrąg Zuzix: W okrąg o promieniu 12 wpisano czworokąt ABCD w taki sposób, że przekątna AC jest średnicą tego okręgu. Wiedząc, że cos∡A =^√58₈ , oblicz długość przekątnej BD. Czy powinnam to rozwiązać w taki sposób że trójkąt DSB gdzie S to środek okręgu jest równoramienny a cos∡S = −^√58₈ a następnie z twierdzenia cosinusów obliczyć długość BD?

xyz: DSB to jest przeciez prosta... (znaczy odcinek) ?

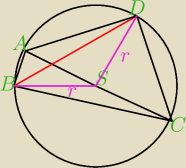
Zuzix: Czemu DSB ma być prostą? Według mnie przykładowy rysunek może wyglądać np. tak

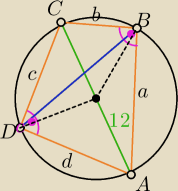
xyz: okej, w sumie zalezy od rysunku. Skad wiesz ile wynosi cosinus kata przy S ?

Zuzix: Teraz jak spojrzałam na swój zapis to źle wyznaczyłam cosinus ale pewnie można go wyznaczyć za pomocą kąta wpisanego i środkowego chociaż nie jestem tego pewna.

xyz: Niech α będzie kątem przy wierzchołku A

	√58
wiadomo, że cos α =		//ułamki za pomocą dużego U.
	8

Kąt środkowy DSB oparty na tym samym łuku co kąt wpisany α ma miarę 2α.

	58		52		13
cos(2α) = 2cos2α − 1 = 2*		− 1 =		=
	64		64		16

wtedy |DB|² = r² + r² − 2*r*r*cos(2α)

	13
|DB|2 = 122 + 122 − 2*12*12*
	16

Czyli w sumie tak jak mówisz.

Zuzix: Ok dzięki za pomoc