 1/ rozwiązując układ równań prostych m i n
otrzymujemy : x= 2k−1 i y= −2k−3
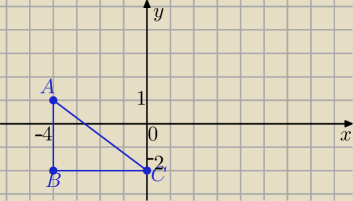
x∊<−4,0> i y∊<−2,1>
to −4≤2k−1≤0 |+1 i −2≤ −2k−3≤1 |+3
−3≤ 2k≤1 i 1 ≤−2k≤4
k∊<−3/2; 1/2> i k∊<−2; −1/2>
wybierając część wspólną
k∊<−3/2;−1/2>
najmniejsze k=−3/2
=======
1/ rozwiązując układ równań prostych m i n
otrzymujemy : x= 2k−1 i y= −2k−3
x∊<−4,0> i y∊<−2,1>
to −4≤2k−1≤0 |+1 i −2≤ −2k−3≤1 |+3
−3≤ 2k≤1 i 1 ≤−2k≤4
k∊<−3/2; 1/2> i k∊<−2; −1/2>
wybierając część wspólną
k∊<−3/2;−1/2>
najmniejsze k=−3/2
=======