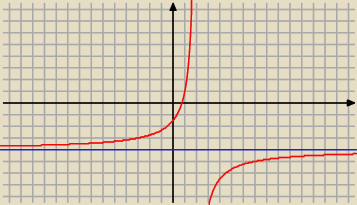
Dany jest wzór funkcji f. Wykaż, że funkcja f jest różnowartościowa: Mateusz: Dany jest wzór funkcji f. Wykaż, że funkcja f jest różnowartościowa:

	4x −3
f(x) =
	2−x

janek191:

Szkolniak:

	4x−3
f(x)=		, x∊D=R\{2}
	2−x

wybieramy dwa dowolne argumenty x₁,x₂∊D takie, że x₁≠x₂

	4x1−3
f(x1)=
	2−x1

	4x2−3
f(x2)=
	2−x2

badamy czy f(x₁)≠f(x₂):

	4x1−3		4x2−3
		≠
	2−x1		2−x2

(4x₁−3)(2−x₂)≠(4x₂−3)(2−x₁) 8x₁+3x₂≠8x₂+3x₁ 8(x₁−x₂)≠3(x₁−x₂) a to jest prawda, ponieważ x₁−x₂≠0, zatem rozpatrywana funkcja jest różnowartościowa.