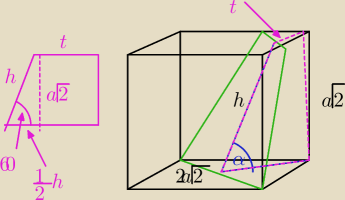
 Graniastosłup prawidłowy czworokątny o krawędzi podstawy 2a i krawędzi bocznej a√2 przecięto
płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod
kątem α. Określ dla jakich α otrzymany przekrój jest trójkątem, a dla jakich trapezem. Oblicz
Graniastosłup prawidłowy czworokątny o krawędzi podstawy 2a i krawędzi bocznej a√2 przecięto
płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod
kątem α. Określ dla jakich α otrzymany przekrój jest trójkątem, a dla jakich trapezem. Oblicz
| π | π | |||
pole przekroju dla α= | i α= | |||
| 6 | 3 |
| a√2 | ||
sin60= | ||
| h |
| 2a√6 | ||
h= | ||
| 3 |
| 1 | 2a√6 | a√6 | ||||
próbowałem coś z "t", że | h= | = | ||||
| 2 | 6 | 3 |
| a√6 | 3a√2 | a√6 | 3a√2−a√6 | |||||
t=a√2− | = | − | = | |||||
| 3 | 3 | 3 | 3 |
 teraz widzisz
teraz widzisz
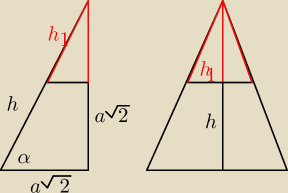
 h (trapezu)=2a√6/3
h (trapezu)=2a√6/3
| a√6 | ||
b=2x x= a√2= | ||
| 3 |
| a√6 | ||
x=a√2− | ||
| 3 |
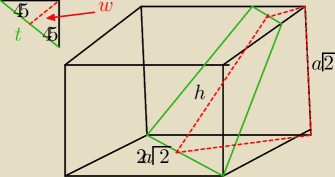 Zapiszę jeszcze co "wskórałem" zanim mi napisaliście:
rozważywszy ten trapez różowy co wcześniej napisałem (tutaj czerwony)
Zapiszę jeszcze co "wskórałem" zanim mi napisaliście:
rozważywszy ten trapez różowy co wcześniej napisałem (tutaj czerwony)
| 1 | a√6 | ||
h= | |||
| 2 | 3 |
| a√6 | 3a√2−a√6 | |||
w=a√2− | = | |||
| 3 | 3 |
|
| |||||||||||||||||||||
P= | = | = | ||||||||||||||||||||
| 2 | 2 |
| 8a2√12−2a2*6 | 1 | 8a2*2√3−12a2 | 1 | |||||
= | * | = | * | =U{16a2√3−1 | ||||
| 3 | 2 | 3 | 2 |
| 1 | 4a2(4√3−3) | 1 | 2a2(4√3−3) | |||||
2a2}{3}* | = | * | = | |||||
| 2 | 3 | 2 | 3 |
