W graniastosłupie prawidłowym o podstawie trójkątnej przekątna ściany bocznej ma kjo21: W graniastosłupie prawidłowym o podstawie trójkątnej przekątna ściany bocznej ma długość d i tworzy z sąsiednią ścianą kąt α. Oblicz objętość graniastosłupa.

salamandra: masz odpowiedź?

Szkolniak:

	d3√3sin2α cosα
Mi wyszło: V=
	4

salamandra:

	√3*sin2α*d2
mi Pp=
	3

	d√(3−4sin2α)*3
H=
	3

Szkolniak: Głupota, zaznaczyłem kąt z krawędzią ściany bocznej a nie z sama ściana boczna

salamandra: Tylko nie wiem jak to "optymalnie" wymnożyć teraz haha

kjo21: Nie mam odpowiedzi. Mógłbym prosić o rysunek?

salamandra:

	h
sinα=
	d

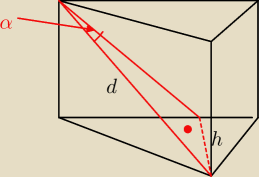
h=sinα*d

a√3
	=h
2

a√3
	=sinα*d
2

a√3=2sinα*d 3a=2√3sinα*d

	2√3sinα*d
a=
	3

	12sin2α*d2		4sin2α*d2
a2=		=
	9		3

	2√3sinα*d   ( )2√3   3		12*sin2α*d2   *√3 9
Pp=		=		=
	4		4

	4√3*sin2α*d2		1		√3*sin2α*d2
=		*		=
	3		4		3

H²+a²=d² H²=d²−a²

	4sin2α*d2		3d2−4sin2α*d2		d2(3−4sin2α)
H2=d2−		=		=
	3		3		3

	d2(3−4sin2α)		d√(3−4sin2α)*3
H=√		=
	3		3

Na razie weź to z przymrużeniem oka, dopóki ktoś nie potwierdzi

a7: https://matematykaszkolna.pl/forum/62258.html

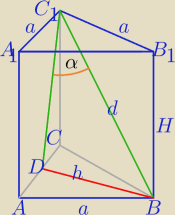
Mila: 1) W ΔBDC₁:

	h
sinα=		⇔h=dsinα
	d

	a√3
2)		=d sinα ⇔a√3=2d sinα
	2

	2dsinα
a=
	√3

	1		1		2dsinα
PΔABC=		*a*h=		*		*dsinα
	2		2		√3

	d2sin2α
PΔABC=
	√3

3) W ΔBCC₁:

	4d2 sin2α
H2+a2=d2 ⇔H2=d2−
	3

	3d2−4d2sin2α		d2*(3−sin2α)
H2=		=
	3		3

	d √3−sin2α
H=
	√3

4)

	d2sin2α		d √3−sin2α
V=		*
	√3		√3

	d3 sin2α*√3−sin2α
V=
	3

======================