Z ćwiartki koła o promieniu 4 utworzono powierzchnię boczną stozka a_psik: Z ćwiartki koła o promieniu 4 utworzono powierzchnię boczną stożka. Jego kąt rozwarcia a(alfa) spełnia warunek A. a>120stopni B. 15stopni<a<30stopni C. a<15 stopni D. 90stopni<a<120stopni

wredulus_pospolitus:

1
	*Obwkoła = Obwpodstawy stożka −−−> r[stożka} =
4

P_{wycinka koła} = P_{b stożka} −−> l_stożka =

	r
sin(α/2) =		−> α/2 w jakim przedziale
	l

a_psik: Nie wiem jak to zrobić, wyszło mi, że r=1 , l=4 α=30

wredulus_pospolitus: Obw_koła = 2πR = 8π

1
	8π = 2π
4

2π = 2πr −−−> r = 1

	1
Pwycinka koła =		πR2 = 4π = πrl −> l = 4
	4

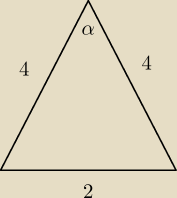
z tw. cosinusów: 2² = 4⁴ + 4⁴ − 2*4*4*cosα 4 = 32 − 64cosα 64cosα = 28

	28		7		1
cosα =		=		<		−−−> 90o > α > 60o
	64		16		2

a_psik: Dziękuję bardzo

piotr: α = 2asin(1/4) ≈ 2*14.48st. ⇒ 15stopni<α<30stopni