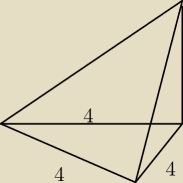
 Podstawą ostrosłupa jest trójkąt równoboczny o boku długości 4. Jedna ze ścian bocznych, będąca
również trójkątem równobocznym, jest prostopadła do płaszczyzny podstawy. Wykonaj rysunek i
oblicz pole powierzchni bocznej ostrosłupa.
Trochę nie rozumiem, bo która ściana będzie również trójkątem równobocznym? I jak może być
jednocześnie równoboczny i prostokątny, skoro ta ściana jest prostopadła do płaszczyzny
podstawy?
Podstawą ostrosłupa jest trójkąt równoboczny o boku długości 4. Jedna ze ścian bocznych, będąca
również trójkątem równobocznym, jest prostopadła do płaszczyzny podstawy. Wykonaj rysunek i
oblicz pole powierzchni bocznej ostrosłupa.
Trochę nie rozumiem, bo która ściana będzie również trójkątem równobocznym? I jak może być
jednocześnie równoboczny i prostokątny, skoro ta ściana jest prostopadła do płaszczyzny
podstawy?
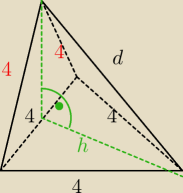
| 4√3 | ||
h = | = 2√3 | |
| 2 |
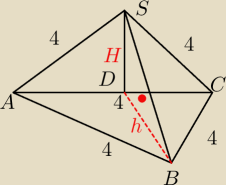 taa, już do tego doszedłem
PACS = 4√3
BS=2√6
Te BCS i ASB to z Herona lecieć, czy jakoś prościej da rade?
taa, już do tego doszedłem
PACS = 4√3
BS=2√6
Te BCS i ASB to z Herona lecieć, czy jakoś prościej da rade?
| 4*√10 | ||
P= | =2√10 | |
| 2 |
| 2√6*√10 | ||
P= | = √60 = 2√15 | |
| 2 |