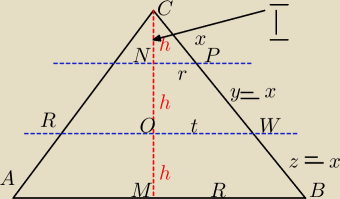
stereometria salamandra: Stożek przecięto płaszczyznami równoległymi do jego podstawy i dzielącymi jego wysokość na n równych części. Udowodnij, że obwody powstałych przekrojów tworzą ciąg arytmetyczny. x+y+z=l Z podobieństwa w trójkątach ΔMBC oraz ΔNPC

3h		h
	=
l		x

3hx=hl 3x=l Znów w tych samych trójkątach

h		3h
	=
r		R

Rh=3Hr R=3r W trójkątach ΔNPC i OWC

h		2h
	=
r		t

ht=2hr t=2r Niech mały stozek na górze to I, średni, tj ograniczony prostą RW to II, a ABC to III L₁=2r+h+x L₂=4r+2h+2x L₃=6r+3h+3x (2r+h+x, 4r+2h+2x, 6r+3h+3x)− ciąg arytmetyczny o różnicy r=2r+h+x Jest ok?

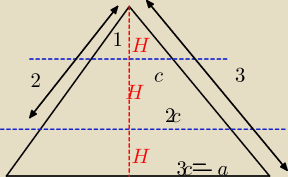salamandra: Od razu dopiszę następne analogiczne, które mi już nie wychodzi: Ostrosłup przecięto dwoma płaszcyznami równoległymi do jego podstawy i dzielącymi jego wysokość na 3 równe odcinki. Udowodnij, że stosunek objętości powstałych brył, licząc od wierzchołka wynosi 1:7:19. Pytanie− jaki ostrosłup, dowolny? No to biorę sobie np. czworokątny prawidłowy. Rysuję przekrój.

	3H		H
Z podobieństwa		=
	a		c

3Hc=aH 3c=a

	4c2*H
V1=
	3

	16c2*2H
V2=
	3

	36c2*3H
V3=
	3

V2		16c2*2H		3
	=		*		=8
V1		3		4c2H

co jest nie tak?

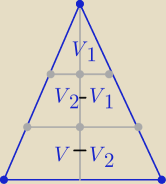Eta: Ostrosłupy są podobne ( nie jest ważne jakie mają podstawy) Stosunek objętości brył podobnych w skali k , jest równy k³

	1
to V1 do V w skali k=1/3 to V1=		V
	27

	8
V2do V w skali k=2/3 to V2=		V
	27

	7
to V2−V1 =		V
	27

	19
oraz V−V2=		V
	27

zatem stosunek objętości tych części jest równy 1:7:19 ======= i po bólu

salamandra: Dziękuję a pierwsze?

Eta: Obwody przekrojów to obwody kół 2πr, 4πr,6πr,.... więc tworzą ciąg arytmetyczny o różnicy 2πr

salamandra: No tak, z przekrojem osiowym mi się troche porąbało. Czyli wystarczy, że rozważyłbym r?

Eta:

salamandra: Dziękuję za dziś, dobranoc

Eta:

an: 1. czy nie łatwiej rys. j/w