... Lilianna: Korzystając z postaci wykładniczej rozwiąż równanie: z³ = |z|³. |z|³ = |r*e^iφ|³ = Nie bardzo wiem, co dalej z tym... Proszę o pomoc.

Leszek: |z| = r z³ = r³*e^3iφ r³*e^3iφ = r³ ⇒ ........

Lilianna: {r³ = r³ {e^3iφ = e^i*0

Adamm: r³e^i3α = r³ r = 0 lub e^i3α = 1 e^i3α = 1 3α = 2πk, k∊Z

	2πk
z = 0 lub (z = rexp(i		, k∊{0, 1, 2}, r>0)
	3

Adamm: czyli rozwiązania są postaci

	2πk
z = rexp(i		), dla r≥0, k∊{0, 1, 2}
	3

Lilianna: Skąd wiadomo że r=0?

Lilianna: Jakie wyszły w ogóle r =? w tym zadaniu?

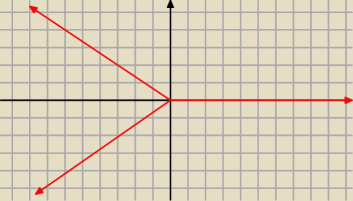
Adamm: r jest dowolne ≥ 0 rozwiązaniami są 3 proste, podobnie jak na rysunku

Lilianna: Aaa, no rzeczywiście. Dziękuję Wam.