Zadania maturalne Jakes:

	f(2x+1)
1. Jeśli f(x) = x3 − x2 + 3x − 5, to		jest równe ?
	2

	π		m2 − 3m + 2
2. Równanie sin( 2x −		) =		ma rozwiązanie dla m należącego
	12		m − 1

do jakiego przedziału ?

	1		f'(1)
3. Jeśli f(x)= x2 −		, to √		jest równe ?
	x2		f'(2)

4. Dany jest trójkąt ABC, w którym |AB|=12, |BC|=8, |AC|= 6. Oblicz cos|∡BAC|. W poniższe kratki wpisz kolejno pierwszą, drugą i trzecią cyfrę rozwinięcia dziesiętnego otrzymanego wyniku. 5. Dany jest trójkąt prostokątny ABC o przyprostokątnych długości |AC|=a i |BC|=b. Dwusieczna kąta prostego przecina przeciwprostokątną w punkcie D.

	√2ab
Uzasadnij, że |CD|=
	a+b

6. Rozwiąż równanie | |√ 4 + x² + 4x | − | x − 3 | | = x 7. Suma trzech liczb dodatnich jest równa 13. Wiadomo, że trzeci składnik jest trzy razy mniejszy niż drugi. Uzasadnij, że spośród liczb spełniających te warunki, suma kwadratów liczb 5,6,2 jest najmniejsza z możliwych. 8. Wyznacz ekstrema lokalne funkcji f(x)= x⁴ * | x + 2|. Bardzo proszę o pomoc

wredulus_pospolitus: 1)

f(2x+1)		(2x+1)3 − (2x+1)2 + 3(2x+1) − 5
	=		= ... liczysz
2		2

wredulus_pospolitus: 2)

	m2 − 3m + 2
−1 ≤		≤ 1 <−−− rozwiąż te nierówności
	m−1

wredulus_pospolitus: 3)

	1
f(x) = x2 −
	x2

f'(x) = ... f'(1) = ... f'(2) = ...

wredulus_pospolitus: 4) wskazówka: Tw. cosinusów

wredulus_pospolitus: 6) |√4 + x² + 4x| = |√(x+2)²| = | |x+2| | = |x+2| rozwiązujesz dalej

Jakes: Jeśli tylko mogę prosić o rozwiązanie do końca 3, bo kompletnie nie czaje, a za resztę wskazówek bardzo dziękuję <3

wredulus_pospolitus: masz liczby x , 3y , y x + 3y + y = 13 −> x + 4y = 13 −> x = 13 − 4y f(x,y) = x² + (3y)² + y² = x² + 10y² = (13 − 4y)² + 10y² = 26y² − 104y + 169 f(y) = 26y² − 104y + 169 y_wierzchołka = ... wniosek

wredulus_pospolitus: 3) a pochodne potrafisz liczyć

wredulus_pospolitus: 8) pochodne się kłaniają

Jakes: Właśnie w tym problem, że niestety nie

wredulus_pospolitus: no to niestety ... musisz się nauczyć liczyć pochodne ... później możesz wrócić do tych zadań

wredulus_pospolitus: więc siadaj do materiałów i się ucz pochodnych ... tego nie da się 'wyjaśnić' w 3 sekundy ... to musisz przerobić ... a przede wszystkim zrobić dziesiątki (jak i nie setki) przykładów na liczenie samej pochodnej

Jakes: Wielkie dzięki za pomoc

Leszek:

	m2 −3m +2
2) napisz nierownosc : −1 ≤ sin α ≤ 1 ⇔ −1 ≤		≤ 1
	m−1

Rozwiaz ta podwojna nierownosc z odpowiednimi warunkami ( m ≠ 1)

	2
3) pochodna : f ' (x) = 2x +		, oblicz ........
	x3

6) √ ( x+2)² = | x+2 | , czyli.| | x +2 | − | x −3| | = x ⇒ | x +2 | − | x− 3 | = x Lub : | x +2 | − | x − 3 | = −x Jest duzo pisania , rozwiaz kazde rownanie z podzialem na przedzialy , Powodzenia !

wredulus_pospolitus: Leszek ... co do 6 ... nie zgodzę się z takim opuszczeniem 'dużego' modułu bez podania warunku: x ≥ 0 co z kolei nosi ze sobą konsekwencję: x+2 > 0

Jakes: Pierwsze mi wyszło 4x³ + 4x² + 4x − 1

Jakes: W drugim obliczyłem m i wyszło, że m=3 tylko teraz nie bardzo wiem co z przedziałem

salamandra:

	m2−3m+2
2)		≥ −1
	m−1

m2−3m+2−m+1
	≥ 0
m−1

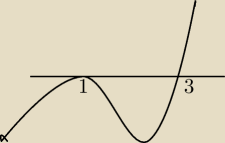
(m²−3m+2−m+1)(m−1) ≥ 0 (m²−4m+3)(m−1)=0 Δ=16−12 = 4 v m=1 m=1 m=3 m∊<3;∞) i analogicznie z drugą nierównością

Jakes: W tej nierówności wyszło mi m∊<1;∞)

salamandra: W "tej" to znaczy której? pokażesz jakieś obliczenia?

Jakes: W tej, którą miałem zrobić analogicznie, tam gdzie jest ≥ −1

Jakes: Nie wiem teraz tylko jak to połączyć

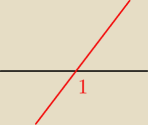
salamandra: Oczywiście popełniłem błąd: Powinno być

m2−3m+2
	≥ −1
m−1

m2−3m+2+m−1
	≥0
m−1

m2−2m+1
	≥0
m−1

(m²−2m+1)(m−1) ≥0 (m²−2m+1)(m−1)=0 Δ=0 v m = 1 m=1 m∊<1;∞)

Jakes: No przecież dobrze mi wyszło to m∊<1;∞)

Jakes: To wtedy to m∊(1;3> ?

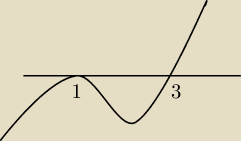
salamandra: i teraz druga

m2−3m+2
	≤1
m−1

m2−3m+2−m+1
	≤0
m−1

m2−4m+3
	≤0
m−1

(m²−4m+3)(m−1)≤0 m=1 v m=1 m=3 m∊(−∞; 3> \ {1} wyciągasz część wspólną dwóch przedziałów

Jakes: Jakby ktoś mógł jeszcze tylko zobaczyc to 3 :cccc

salamandra:

	1
f(x)=x2−
	x2

	2x4+2
f'(x)=
	x3