Czworokąt wpisany w okrąg - geometria analityczna
xyz: Czworokąt UVWZ jest wpisany w okrąg. Przekątna o końcach U=(−3, 4) i W=(−1,−2) przechodzi przez
środek okręgu, zaś dwa boki czworokąta zawierają się w prostych o równaniach: x+y+3=0
i x+2y−5=0. Wyznacz równania ogólne prostych zawierających pozostałe boki czworokąta.
Próbowałem zrobić to zadanie w taki sposób:
1. Policzenie środka odcinka |UW| − ten środek oznaczyłem jako S wydawało mi się, że jest
to środek okręgu opisanego na czworokącie.
S = ( (−3−1)/2, (4−2)/2)
S = (−2, 1)
2. Próbowałem policzyć promień okręgu, czyli długość odcinka |US|, ale wyszedł mi promień
√10. −>
R = |US|
|US| =
√(−2+3)2 + (1−4)2 =
√1+9 =
√10
R =
√10
Tutaj się zatrzymałem, bo być może mój tok myślenia odnośnie punktu S jest błędny. Czy
ten punkt S rzeczywiście jest w tym przypadku środkiem okręgu opisanego na tym czworokącie?
Trochę nie mam pomysłu na to zadanie. Próbowałem wyznaczyć promień i nanieść rysunek
na układ współrzędnych, żeby zobaczyć w tym zadaniu coś więcej, ale promień niestety nie
jest liczbą całkowitą albo moje myślenie jest błędne.
Byłbym wdzięczny za pomoc.
16 mar 21:14
Tadeusz:
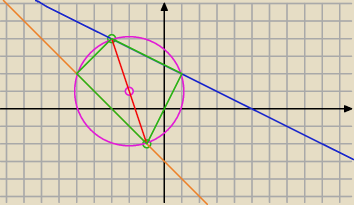
16 mar 21:30
Tadeusz:
... dawaj dalej bo dobrze myślisz
16 mar 21:34
Eta:
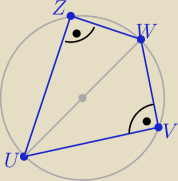
Ale nawydziwiałeś !
sprawdzamy który z punktów należy do danych prostych
do prostej x+y+3=0 należy punkt W ( dlaczego?
do prostej x+2y−5=0 należy punkt U
zatem prosta VW: x+y+3=0 ⇒ y= −x−3
| | 1 | | 5 | |
zaś prosta UZ: x+2y−5=0 ⇒ y= − |
| x+ |
| |
| | 2 | | 2 | |
to prosta ZW ⊥UZ i prosta UV ⊥VW
zatem ......
dokończ
16 mar 21:35
Eta:
Tadeusz ..... piłeś coś?
16 mar 21:37
a7:
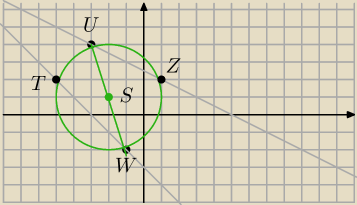
R=
√10 R to polowa odległości między punktami U i W S=(−2,1)
T=(x
T,−x
T−3)
Z=(x
Z,−1/2x
Z+5/2)
|ST|=
√10 √(−2−xt)2+(−xT+4)2=
√10 Δ=64 x=−5 lub x=−1 (x=−1 jest dla punktu W)
x=−5 y=2
T(−5,2)
Z liczymy tak samo jak T
Z=(1,2)
16 mar 21:42
Tadeusz:
dlsczego tak sądzisz?
Nie rozwiązuję zadań tylko podpowiadam ... pyta o to czy S jest środkiem okręgu opisanego ...
Dalej niech kuma ... Rysunek pokazuje co dalej ... warunek prostopadłości i prosta przez punkt
16 mar 21:42
Tadeusz:
do równań o które pytają nie potrzebuje pozostałych punktów
16 mar 21:44
Tadeusz:
... a swoją drogą jak dotąd w podlaskiem nie mamy "korony" bo dezynfekcja zewnętrzna
jak i wewnętrzna "duchem puszczy" obala korony
16 mar 21:49
Eta:
16 mar 21:59
a7: to dla mnie?
16 mar 21:59
Eta:
Też może być i dla Ciebie
16 mar 22:01
a7:
16 mar 22:02
Eta:
Teraz dla Ciebie ...
16 mar 22:02
Kamil: Dziękuję Wam!
16 mar 22:14