Własnosci prawdopodobienstwa Patryk: Zdarzenia A i B są podzbiorami zbioru zdarzen element. omega pewnego doświadczenia. Wiedząc,

	5		2
że P(A') ≥		uzasadnij ,że P(A' ∪ B) >
	7		3

Nie za bardzo ogarniam jak wyglądają te zbiory, czy mógłby mi ktoś naszkicować na rysunku jak wygląda zbiór P(A') oraz P(A' ∪ B) uwzględniając, że w zbiorze omega są te dwa podzbiory czyli A oraz B?

wredulus_pospolitus: Ale w sumie ... co tu udowadniać

	5		2		2
P(A' u B) ≥ P(A') ≥		>		−−−> P(A' u B) >
	7		3		3

c.n.w.

Patryk: Wiem Ale chciałem na rysunki zobaczyć jak te zbiory wyglądają żeby łatwiej mi było sobie wyobrazić sytuacje tego typu

Tito: Tutaj jest taki problem, że ciężko to narysować. Możesz mieć różne sytuacje: np P(B)=0, P(A') też może zajmować różne części przestrzeni więc lepiej przeanalizuj tym razem sam dowód wredulusa.

Patryk: To tylko zapytam słownie, zbiór A' to taki który leży po za A i B natomiast A'∪B to taki który nie zawiera A, ale zawiera już B?

Tito: A' to całe"pole" poza A. A'∪B natomiast to całe "pole" nie zawierające A i całe "pole" B. Możesz mieć taki przypadek, że np B ma część wspólną z A i wtedy w A'∪B to A też się zawiera częściowo. Najlepiej to zaznaczaj tak, że bierzesz całe A' czyli wszytko poza A a później B czyli całe B(nie isteresuje cię co w nim jest ). To o czym ty napisałeś to "taki który nie zawiera A, ale zawiera już B" to jest część wspólna A' i B czyli odwrotnie ten znaczek musi być.

Tito: Podręcznik 3 klasa Kurczaba sobie ogarnij. Tam to jest bardzo fajnie wytłumaczone.

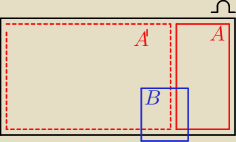
wredulus_pospolitus: A' u B to będzie to co jest w A' i w B (czyli całe A' plus (A n B) )

Patryk: Czy na pewno? Bo jeśli jest suma zdarzeń czyli "lub" to chyba w tym przypadku część A ∩ B biorę natomiast część wspólną A' i B przy sumie chyba odrzucam