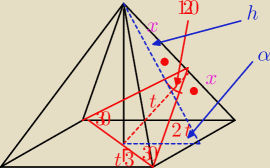
 Kąt dwuścienny między dwiema sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego
ma miarę 120 stopni. Wykaż, że kąt nachylenia ściany bocznej do płaszczyzny podstawy jest
równy 45.
W trójkącie czerwonym: t, 2t, t√3
przekątna podstawy (a√2) = 2t√3
2t√6=2a
a=t√6
Jakaś podpowiedź?
Oraz czy ten odcinek 2t (wysokość ściany bocznej?) będzie równa h? czy wysokości w trójkącie
równoramiennym są równe? oraz czy WSZYSTKIE wysokości trójkąta równoramiennego dzielą odcinek
(podstawę) na połowę (odcinki x)?
Kąt dwuścienny między dwiema sąsiednimi ścianami bocznymi ostrosłupa prawidłowego czworokątnego
ma miarę 120 stopni. Wykaż, że kąt nachylenia ściany bocznej do płaszczyzny podstawy jest
równy 45.
W trójkącie czerwonym: t, 2t, t√3
przekątna podstawy (a√2) = 2t√3
2t√6=2a
a=t√6
Jakaś podpowiedź?
Oraz czy ten odcinek 2t (wysokość ściany bocznej?) będzie równa h? czy wysokości w trójkącie
równoramiennym są równe? oraz czy WSZYSTKIE wysokości trójkąta równoramiennego dzielą odcinek
(podstawę) na połowę (odcinki x)?
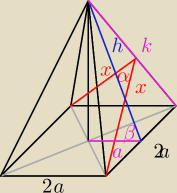
| a | ||
sinβ= | ||
| h |
| 1 | 1 | ||
xk= | 2ah | ||
| 2 | 2 |
| 2√6 | ||
x= | a | |
| 3 |
| 2√6 | |
a*k=2ah | |
| 3 |
 może ktoś wyłapie błąd
dalej posługując się moim rysunkiem:
x2+(2t)2=(t√6)2
x2+4t2=6t2
x2=2t2
x=t√2
t√6 to krawędź podstawy.
może ktoś wyłapie błąd
dalej posługując się moim rysunkiem:
x2+(2t)2=(t√6)2
x2+4t2=6t2
x2=2t2
x=t√2
t√6 to krawędź podstawy.
| 2*t√2*2t | ||
PΔ (ściany bocznej)= | = 2t2√2 | |
| 2 |
| t√6*h | ||
ale również PΔ= | ||
| 2 |
| t√6*h | ||
2t2√2= | / * 2 | |
| 2 |
| 4t2√2 | |
=h | |
| t√6 |
| 4t√2 | |
=h | |
| √6 |
| 4t√12 | ||
h= | ||
| 6 |
| 4t*2√3 | 8t√3 | 4t√3 | ||||
h= | = | = | ||||
| 6 | 6 | 3 |
| t√6 | 3 | 3√6 | 3√18 | 3*3√2 | ||||||
cosα= | * | = | = | = | = | |||||
| 2 | 4t√3 | 8√3 | 8√3 | 24 |
| 9√2 | 3√2 | |||
= | ||||
| 24 | 8 |
 Salamandra nie jest to prawdą
Salamandra nie jest to prawdą
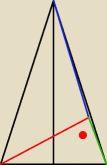 Sam możesz to zobaczyć. Ściany boczne to trójkąty równoramienne (zobacz rysunek).
Sam możesz to zobaczyć. Ściany boczne to trójkąty równoramienne (zobacz rysunek).
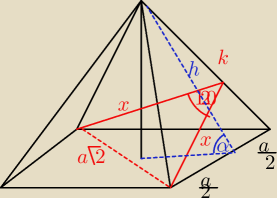 Nie wychodzi mi:
Nie wychodzi mi:
| 1 | kx | |||
P= | *kx= | |||
| 2 | 2 |
| 1 | ah | |||
P= | *a*h= | |||
| 2 | 2 |
| 2 | |
a2=x2 | |
| 3 |
| 2 | √2 | a√6 | ||||
x=√ | a2=a | = | ||||
| 3 | √3 | 3 |
| 1 | a√6 | ah | |||
*k* | = | ||||
| 2 | 3 | 2 |
| k*a√6 | ah | ||
= | / * 6 | ||
| 6 | 2 |
| k√6 | ||
h= | ||
| 3 |
| 1 | k√6 | |||
( | a)2+( | )2=k2 | ||
| 2 | 3 |
| 1 | 6k2 | ||
a2+ | =k2 | ||
| 4 | 9 |
| 1 | 2k2 | ||
a2+ | =k2 | ||
| 4 | 3 |
| 1 | 1 | ||
a2= | k2 | ||
| 4 | 3 |
| 4 | ||
a2= | k2 | |
| 3 |
| 2k | 2√3k | |||
a= | = | |||
| √3 | 3 |
| 2√3k | 3 | 2√3 | √3 | √18 | 3√2 | |||||||
cosα= | * | = | = | = | = | = | ||||||
| 6 | k√6 | 2√6 | √6 | 6 | 6 |
| √2 | ||
| 2 |
| a | ||
znaczy wychodzi, kapnąłem się pod koniec jak tu pisałem, bo wziąłem zamiast | , całe a, i | |
| 2 |
 dzięki Saizou
dzięki Saizou
