geometria analityczna Gangster: przekatna kwadratu opisanego na okregu o rownaniu x²+y²−2x−4=0 zawiera sie w prostej o rownaniu 2x−y−2=0. Wyznacz wspolrzedne wierzcholkow tego kwadratu. Okrag ten mam jako S (1,0) r²=5 okrag OPISANY na kwadracie jako S (1,0) i R²=10 gdy podstawiam podana prosta do rownania okregu Opisanego, czyli tam gdzie wlasnie te wierzchołki są wychodza mi wspolrzedne

2+√5		2−√5
	i		a odp sa znowu inne...
2		2

Jerzy: Pokaż jak liczysz.

Gangster: do rownania okregu (x−1)² +y² =10 podstawiam y=2x−2 i wychodza mi pierwiastki jakie napisalem wyzej, co jest sprzeczne z odp

wredulus_pospolitus: (x−1)² + y² = 5 <−−− skąd niby R² = 10

wredulus_pospolitus:

	√5
ok ... opisany ma r = √5 −−−> a =		−−−> R = √10 ... okey
	2

Gangster: R² dlatego ze to rownanie okregu OPISANEGO a nie wpisanego

wredulus_pospolitus: no i jak wyznaczasz współrzędne punktów

salamandra: x²+y²−2x−4=0 S(1,0) r=√1²+0²+4 = √5 r²=5 bok kwadratu = 2r = 2√5 długość przekątnej: 2√5*√2= 2√10 okrąg OPISANY:

	1
R=		d = √10
	2

salamandra: prosta: 2x−y−2=0 y=2x−2 A(x,2x−2) Odległość od A do S to ile

Gangster: x² −2x +1 +4x² −8x +4=10 5x² −10x −5=0 x²−2x−1=0 i wychodza powyzsze pierwiastki

Gangster: salamandra dzieki ale napisales dokladnie to co juz napisalem na poczatku

Gangster: bo wierzcholkami beda punkty przeciecia OPISANEGO z podana prosta, czy nie?

salamandra: |AS|²=(1−x)²+(2x−2)² = 1−2x+x²+4x²−8x+4 = 5x²−10x+5 5x²−10x+5=10 5x²−10x−5=0 x²−2x−1=0 Δ=4+4=8

	2−2√2
x1=		= 1−√2
	2

x2=1+√2 A(1−√2; 2(1−√2)−2)= (1−√2; −2√2) no i jakiś np. C, to współrzedne tego drugiego, o ile sie nigdzie nie machnąłem

Gangster: Czyli klasyczny moj blad, wszystko dobrze rozumiem, złe rachunki...

salamandra: dobrze mi wyszło?

Gangster: tak

salamandra:

Gangster: z dodawania 4+4 wyszlo mi 5i dlatego nie moglo mi wyjsc...

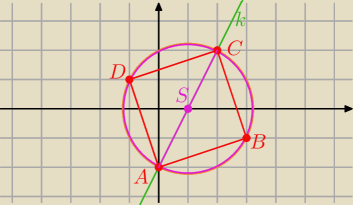
Eta: 1/ S(1,0) r=√5 rozwiązując układ równań okręgu i prostej k: y=2x−2 (x−1)²+(2x−2)²=5 ⇒ 5x(x−2)=0 ⇒ x=0 v x= 2 to y=−2 v y=2 A(0,−2), C( 2,2) ============= 2/ Prosta p= DB ⊥AC ma równanie p:y=−0,5x+0,5 rozwiązując układ równań p i okręgu otrzymasz B( 3,−1), D(−1,1) ============== lub 2/ z własności wektorów prostopadłych......

salamandra: Eta, promień okręgu OPISANEGO to √10

Eta: Ajjjjjjjjj sorry przeczytałam okrąg opisany na kwadracie