Dany jest równoległobok ABCD. Zapisz jako jeden wektor:
zenek:
a) BD − CD
b) AB+BC+CD+DA
c) CD+AC−CB
Dostałem już wczoraj odpowiedź, że powinienem odczytać to z rysunku, jednak dalej szczerze
zbytnio nie wiem jak.

Czy byłby ktoś w stanie wytłumaczyć mi jak to czytać, zapisać?
16 mar 16:25
wredulus_pospolitus:
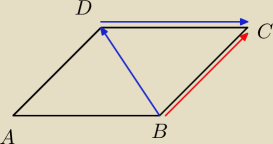
BD − CD = BD
+ DC = BC
analogicznie pozostałe podpunkty
16 mar 16:28
zenek: w takim razie czy to idzie tak −
b) AB+BC=AC+CD=AD+DA= 2AD?
16 mar 16:35
wredulus_pospolitus:
Nie
AD + DA = AD
− AD =

16 mar 16:37
zenek: a w c?
czy CD+AC to to samo co AC+CD=AD?
jeśli tak, to jak od tego odjąć CB?
nie wiem czemu, ale nadal jakoś tak przez mgłę to wszystko
16 mar 16:43
wredulus_pospolitus:
CD + AC tak ... to to samo co AC + CD = AD
CB = DA

.... wektory można sobie 'przesuwać' w pionie lub poziomie
Wektor CB mówi tyle samo co wektor DA (bo DA || CB)
16 mar 16:45
zenek: i co zapisac w tej odpowiedzi w b? haha, brak?
16 mar 16:46
zenek: aha, okej
16 mar 16:46
wredulus_pospolitus:
w (b) ... wektor ZEROWY (pamiętasz jak się go zaznacza

)
16 mar 16:48
zenek: Niestety nie, są to zadania które muszę sam ogarnąć, ze względu na obecną sytuację. Miałem
tylko jedną lekcje w szkole o wektorach, na której nie było nic mówione o wektorze zerowym.
16 mar 16:49
wredulus_pospolitus:
→
0
w taki sposób
16 mar 16:50
zenek: okej

, dziękuję bardzo za pomoc
16 mar 16:50
16 mar 16:52
 Czy byłby ktoś w stanie wytłumaczyć mi jak to czytać, zapisać?
Czy byłby ktoś w stanie wytłumaczyć mi jak to czytać, zapisać?
 BD − CD = BD + DC = BC
analogicznie pozostałe podpunkty
BD − CD = BD + DC = BC
analogicznie pozostałe podpunkty

 .... wektory można sobie 'przesuwać' w pionie lub poziomie
Wektor CB mówi tyle samo co wektor DA (bo DA || CB)
.... wektory można sobie 'przesuwać' w pionie lub poziomie
Wektor CB mówi tyle samo co wektor DA (bo DA || CB)
 )
)
 , dziękuję bardzo za pomoc
, dziękuję bardzo za pomoc