pochodna salamandra: Czy pochodną tego:

	r3√3
−		liczy się jako pochodną ilorazu? Photomath mówi, że to będzie −√3r2, a ja bym
	3

to rozpisał pewnie na pochodną ilorazu i wyszloby mi:

−√3r3*3		−√3r3
	=
9		3

Jerzy: Nie,stałą wyciągasz przed pochodną: [a*f(x)]’ = a*f’(x)

salamandra: aha, rozumiem, dzieki

salamandra: czyli ta pochodna ilorazu ma zastosowanie tylko, gdy w mianowniku występuje zmienna?

Jerzy: Nie,możesz liczyć ze wzoru na iloczyn i wynik będzie dobry, tylko po co ?

Jerzy: Tfuu ... na iloraz.

salamandra: no właśnie jak widzisz− spróbowałem i nie wyszło

salamandra: ok, widzę błąd, nie pomnożyłem licznika jeszcze *3

wredulus_pospolitus: iloraz ... iloczyn ... bez różnicy zresztą wzór na pochodną ilorazu wynika ze wzoru na pochodną iloczynu

salamandra: a nie, pomnożyłem, więc no, nie wiem gdzie błąd

salamandra:

	r3√3
−		=f(x)
	3

	3√3r2		√3r2
f'(x)=−		= −
	9		3

Jerzy:

	1		x
Policz pochodną z f(x) =		*x, a potem z f((x) =		korzystając ze wzoru na pochodną
	3		3

ilorazu.

wredulus_pospolitus:

	r3√3
f(r) = −
	3

ze wzoru [ a*f(r) ]' = a*f'(r)

	√3
f'(r) = −		(r3)' = −√3r2
	3

lub

	f		f' * g − f * g'
ze wzoru [		]' =		(gdzie g(r) = 3)
	g		g2

	−3√3r2*3 − 0*√3r3		−9√3r2
f'(r) =		=		= −√3r2
	32		9

lub

	1
ze wzoru [f*g]' = f' * g + f * g' (gdzie g(r) =		)
	3

f'(r) = ( (−√3r³)*(1/3) )' = −3√3r²*(1/3) + (−√3r³)*0 = −√3r²

Jerzy: 16:22 źle stosujesz wzór na pochodną ilorazu.w mianowniky masz funkcję stałą i jej pochodna to 0.

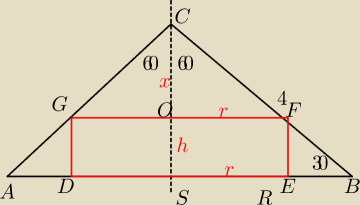
salamandra: wszystko jasne, jednak zgubiłem jedno *3 przejdę do rzeczy: zadanie: Dany jest stozek o kącie rozwarcia 120 i tworzącej dlugosci 4. Oblicz objętość tego walca wpisanego w dany stożek, którego pole powierzchni bocznej jest największe. 1) z trójkąta 30,60,90 H=2 R=2√3 2) h∊(0;2) r∊(0;2√3) z podobieństwa w trójkątach SBC oraz OFC

	x
U{2}{2√3=
	r

x*2√3=2r

	2r		r√3
x=		=
	2√3		3

	r√3
h=2−
	3

	r√3		r2√3
Pb=2πr*h = 2π*r*(2−		) = 2π*(2r−		)
	3		3

	−r2√3
f(r)=		+2r
	3

	−r2√3
f(r)=0 ⇔		+2r = 0
	3

−r2√3
	+2r=0
3

	r√3
−r(		−2)=0
	3

	r√3
r=0 v		=2 / * 3
	3

r√3=6 3r=6√3 r=2√3

	2√3*√3
h=2−		=2−2=0
	3

salamandra: idiota.. przecież ja policzyłem miejsca zerowe tej paraboli, i wziąłem r z miejsca zerowego a nie z wierzchołka...

wredulus_pospolitus: do wyznaczeni P_b ... oki f(r) <−−− i co się tutaj dalej dzieje

salamandra: a<0 więc wartość największa dla WIERZCHOŁKA, a nie miejsca zerowego (poleciałem z automatu jakbym pochodną to robił), więc dla "p"

	−2		3		3		3√3
p=		= −2*		=		=		= √3
	−2√3   3		−2√3		√3		3

r=√3

	√3*√3
h=2−		= 2−1=1
	3

V=π*3*1=3π

wredulus_pospolitus: jest ok

salamandra: dzieki