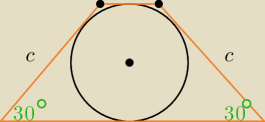
Pole powierzchni trapezu pokazanego na rysunku wynosi 10. licealista: Pole powierzchni trapezu pokazanego na rysunku wynosi 10. Oblicz wysokość tego trapezu

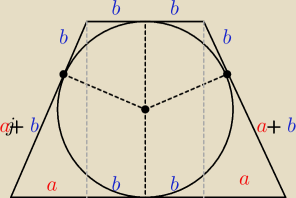wredulus_pospolitus: z funkcji trygonometrycznych:

	a		√3
cos30o =		=		−> a = ...*b
	a + 2b		2

w takim razie a+2b = .... *a

	h		1
sin30o =		=		−−−> h = ...*a
	a+2b		2

	(2a+2b+2b)
P =		*h = 10 −−−> a = .... −−−> h = ....
	2

licealista: Niezbyt rozumiem ten twój zapis

wredulus_pospolitus: a czego KONKRETNIE nie rozumiesz

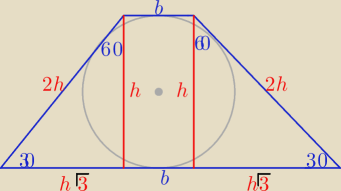Eta: Na rys. oznaczenia z trójkątów "ekierkowych" o kątach ostrych 30^o i 60^o Z warunku wpisania okręgu w trapez : 4h=2h√3+2b ⇒ 2h=h√3+b P=(h√3+b)*h =10 ⇒ 2h²=10 , h>0 h=√5 ======