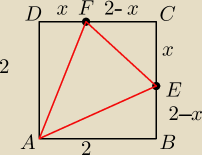
optymalizacja salamandra: Dany jest kwadrat ABCD o boku równym 2. Na bokach BC i CD wybrano odpowiednio punkty E i F, różne od wierzchołków kwadratu, takie że CE=DF=x. Oblicz wartość x, dla której pole trójkąta AEF jest najmniejsze. Oblicz to pole. Zrobiłem tak, że rozważyłem trzy trójkąty. ΔABE

	1
P=		*2*(2−x)=−x+2
	2

ΔECF

	1		1		1
P=		*x*(2−x)=		x*(2−x)=−		x2+x
	2		2		2

ΔADF

	1
P=		*2*x=x
	2

Pole tych trzech:

	−1		1		−1
P=x+(		x2+x)+(−x+2)=2x−		x2−x+2=		x2+x+2
	2		2		2

Pole tych trzech będzie największe w wierzchołku

	−1
p=		=1
	−1

dla x=−1 pole tych trzech trójkątów będzie największe, czyli wtedy pole AEF będzie najmniejsze. Pole kwadratu= 4

	−Δ		−5
Pole tych trzech trójkątów dla x=1, to rzędna wierzchołka q=		=		=2,5
	4a		−2

Więc pole AEF=4−2,5=1,5 Jest ok, czy można bylo inaczej?

wredulus_pospolitus: Proszę mi powiedzieć ... w jakim przedziale może się znaleźć x Proszę podać długość odcinka CE dla wyznaczonego przez Ciebie 'x'

salamandra: Tak, x∊(0;2), w zeszycie napisałem

wredulus_pospolitus: a jaki 'x' wychodzi Ci x = −1

Jerzy: x = − 1 ( jakim cudem , skoro to odległość ? )

salamandra: x=1, literówka, sory

wredulus_pospolitus: Na jedno wychodzi ... może troszeczkę szybciej:

	2*(2−x)		2*x
P(ABE) + P(ADF) =		+		= (2−x) + x = 2 (pole jest stałe, nie zależy od
	2		2

'x')

	x(2−x)
P(ECF) =		(tylko to pole zależy od 'x')
	2

	0 + 2
Maksimum dla xwierzchołka =		= 1
	2

	x(2−x)		x(2−x)		1*1
P(AEF) = 4 −		− 2 = 2 −		= 2 −		= 1.5
	2		2		2

salamandra: Dzięki