dowody w geometrii
Alina: Witam.
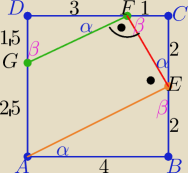
Punkt E jest środkiem boku BC kwadratu ABCD o boku długości 4.
Punkt F dzieli bok CD tego kwadratu w stosunku |DF| : |FC| = 3 : 1.
Przez punkt F poprowadzono równoległą do odcinka AE, która przecięła
bok AD w punkcie G (zobacz rysunek). Wykaż, że trapez AEFG jest
prostokątny i oblicz długość jego dłuższego ramienia.
https://imgur.com/a/fw5OloE
wredulus_pospolitus:
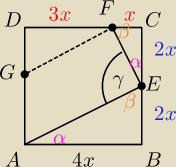
Z podobieństwa trójkątów ΔABE i ΔECF (podobieństwo KKK)
mamy: γ = 180 − α − β = 180 − (180 − 90) = 90
o <−−− kąt prosty
Z faktu, że FG || AE wynika, że AEFG jest trapezem (co jest podane w zadaniu), wynika także,
że
∡GFE = 180 − γ = 90
o
Z tego wynika, że ∡GFD = α
Czyli ΔFDG podobny do ΔECF i ΔABE
poprzez proporcje wyznaczamy długość |DG|
| |DG| | | |FC| | | |DG| | | x | |
| = |
| ⇔ |
| = |
| ⇔ |DG| = 1.5x |
| |DF| | | |CE| | | 3x | | 2x | |
czyli |AG| = 4x − 1.5x = 2.5x .... |AB| = 4x = 4 −−−> x = 1 −−−> |AG| = 2.5
