Punkty A=(2,3), B=(-4,-1) są wierzchołkami równoległoboku...
zenek: Punkty A=(2,3), B=(−4,−1) są wierzchołkami równoległoboku, a punkt S=(2,0)−punkt przecięcia się
przekątnych.
a) wyznacz współrzędne wierzchołków C i D.
b) środki boków równoległoboku połączono odcinkami, oblicz współrzędne wierzchołków otrzymanego
czworokąta i jego obwód.
15 mar 15:58
janek191:
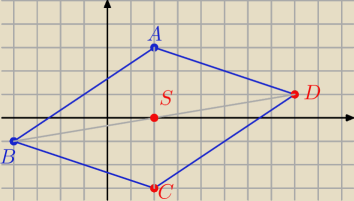
Skorzystaj z tego, że S = ( 2, 0) jest środkiem odcinków: AC i BD.
15 mar 16:06
a7:
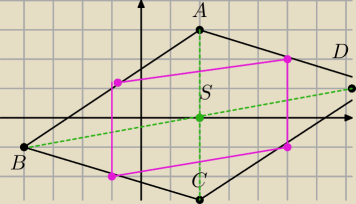
15 mar 16:08
wredulus_pospolitus:
a)
Krok 1: wyznaczasz prostą przechodząca przez A i S
Krok 2: wyznaczasz punkt C będący odległy od punktu S o odległość |AS| i leżący na wyznaczonej
prostej
Krok 3−4: Analogicznie punkt D
b)
Krok 1: Wyznaczasz środki odcinków: AB, BC, CD i AD
Krok 2: wyznaczasz długości odcinków KL, LM, MN, KN wprost ze wzoru na długość odcinka, albo
| | 1 | |
zauważasz, podobieństwo trójkątów (np. ΔABD o Δ AKN) i zauważasz, że |KN| = |
| |BD| = |LM| |
| | 2 | |
(analogicznie druga para odcinków) ... więc obwód = |BD| + |AC|
15 mar 16:08
jc:
C=2S−A=2*(2,0)−(2,3)=(2,−3)
D=2S−B=2*(2,0)−(−4,−1)=(8,1)
15 mar 16:08
janek191:
Np. B =( −4, −1) D = ( x, y)
więc
| | −1 + y | |
U{− 4 + x}[2} = 2 i |
| = 0 |
| | 2 | |
−4 + x = 4 i −1 + y = 0
x = 8 i y = 1
D = ( 8, 1)
========
15 mar 16:09
zenek: Wyznaczyłem, że C = (2,−3), a D = (8,1).
Obliczyłem również wierzchołki − pomiędzy AB − K − (−1,1), pomiędzy CD − L − (5,−1), pomiędzy
BC − N − (−1,−2) i pomiędzy DA − M − (5,2).
Żeby obliczyć obwód, muszę po prostu pomnożyć przez 2 długość KL i długość NM?
15 mar 16:14
zenek: ojej, nie zauważyłem, że dostałem już odpowiedź wyżej, dzięki
15 mar 16:15
zenek: źle przeczytałem, myślałem, że muszę obliczyć obwód równoległoboku
15 mar 16:16
salamandra: mi wyszedł obwód 6+2√37
15 mar 16:40
 Skorzystaj z tego, że S = ( 2, 0) jest środkiem odcinków: AC i BD.
Skorzystaj z tego, że S = ( 2, 0) jest środkiem odcinków: AC i BD.
