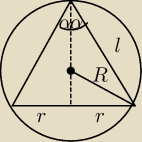
stereometria salamandra: Stosunek pola powierzchni bocznej stożka do pola powierzchni kuli opisanej na tym stożku wynosi 3:8. Wyznacz miarę kąta rozwarcia tego stożka Pb=πrl Pk=4πR² 3πrl=32πR²

r		l
	=
sinα		sin90

r=l*sinα 3πl*sinα*l=32πR² 3l²*sinα=32R² brakuje mi pomysłu co dalej, o ile w ogóle to jest przydatne co zrobiłem

Patryk: Pb = πrl

πrl		3
	=
4πR2		8

2rl = 3R²

	3R2
r =
	2l

musisz teraz literki r, R i l uzależnić od funkcji trygonometrycznych(sin, cos, tg) i

	3R2
podstawiasz do tego równania, które wyszło ze stosunki czyli: r =		. I na końcu
	2l

musisz sprowadzić utworzne równanie do takiej postaci, że była jedna konkretna funkcja np. sin i rozwiązujesz już dalej normalnie

ite: A ja proponuję dodać jeszcze jedno równanie z tymi samymi niewiadomymi l i R. Wykorzytaj tw. sinusów dla trójkąta równoramiennego.

salamandra: Nie rozumiem Patryk, co mi da r=sinα*l R nawet nie wiem jak

	r
l=
	sinα

Patryk: Z twierdzenia sinusów masz:

2r
	= 2R
sin2α

r = R*sin2α Teraz uzależniam l i R

l
	= 2R
sin(90−α)

l = 2Rcosα podstawiam do równania:

	3*R2
R*sin2α =
	2*2*Rcosα

	3
sin2α =
	4cosα

i z tego wyliczyć kąt, jesli się nigdzie nie pomyliłem

salamandra:

	l
czemu		? z którego trójkąta korzystasz
	sin(90−α)

salamandra: ok, już widzę

salamandra: Po prostu chodzi o to, żeby wszystko za pomoca jednej niewiadomej (R) wyznaczyć i później kombinować?

salamandra:

	3
sin2α=
	4cosα

	3
2sinαcosα=		/ * 4cosα
	4cosα

8sinαcos²α=3 8sinα(1−sin²α)=3 8sinα−8sin³α=3 co dalej?

Patryk: Rozkładasz tak jak wielomian, podstaw sobie s = sinα i szukasz miejsca zerowego , jak nie będzie całkowitych to wymierne

salamandra: pustka kompletna dziś, czego się nie dotknę, to nie potrafię rozwiązać...

Szkolniak: −8sin³α+8sinα−3=0 8sin³a−8sinα+3=0 t=sinα 8t³−2t−6t+3=0 2t(4t²−1)−3(2t−1)=0 2t(2t+1)(2t−1)−3(2t−1)=0 (2t−1)[2t(2t+1)−3]=0 (2t−1)(4t²+2t−3)=0

salamandra: dzięki, już to zrobiłem wielomiany akurat ogarniam (nawet dziś)