Prostokąt- kąty
Rafka: W prostokącie ABCD punkt M jest środkiem boku AD, punkt N środkiem boku BC. Na przedlużeniu
odcinka CD poza pukt D wybrano punkt P. Niech S będzie punktem przecięcia prostych PM i AC,
Udowodnij, że ∡SNM=∡MNP.
Ktoś pomoże bo próbowałam i nie mogę nic sensownego wymyslić ?
15 mar 10:00
a7:
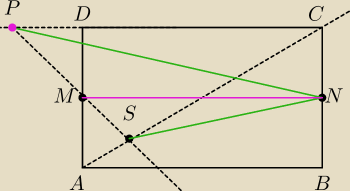
z rysunku mi nie wynika ta równość, czy dobry mam rysunek albo czy dobrze przepisałaś zadanie?
15 mar 11:15
a7: a już widzę
15 mar 11:22
Rafka: Dobrze jest narysowne jednak nie wiem jak to dowieść próbowałam już róznych sposobów

15 mar 13:01
a7: ja na razie nie wiem
15 mar 13:03
ite: Też próbowałam i też nieskutecznie. Ma ktoś pomysł na to zadania?
15 mar 21:39
Eta:
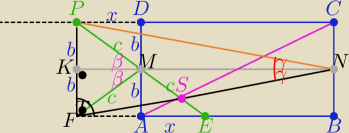
Teraz trzeba dodać odpowiedni komentarz
1/ ΔAME i DMP −− przystające z cechy ....
2/w ΔPFE FM −− dł. środkowej |FM|=c
to ΔPMF −− równoramienny ⇒prosta KM jest dwusieczną
co daje tezę bo prosta MN też jest dwusieczną kąta SNP
15 mar 23:34
Rafka: Dlaczego NF przechodzi przez punkt S?
16 mar 11:33
ite: dziękuję za rozwiązanie!
16 mar 20:39
a7: ja też dziękuję

@Rafka odcinka SF mogłoby tam w ogóle nie być na rysunku
16 mar 20:43
Eta:
Mogłoby ( ale ja sobie dorysowałam

16 mar 20:50
 z rysunku mi nie wynika ta równość, czy dobry mam rysunek albo czy dobrze przepisałaś zadanie?
z rysunku mi nie wynika ta równość, czy dobry mam rysunek albo czy dobrze przepisałaś zadanie?

 Teraz trzeba dodać odpowiedni komentarz
1/ ΔAME i DMP −− przystające z cechy ....
2/w ΔPFE FM −− dł. środkowej |FM|=c
to ΔPMF −− równoramienny ⇒prosta KM jest dwusieczną
co daje tezę bo prosta MN też jest dwusieczną kąta SNP
Teraz trzeba dodać odpowiedni komentarz
1/ ΔAME i DMP −− przystające z cechy ....
2/w ΔPFE FM −− dł. środkowej |FM|=c
to ΔPMF −− równoramienny ⇒prosta KM jest dwusieczną
co daje tezę bo prosta MN też jest dwusieczną kąta SNP
 @Rafka odcinka SF mogłoby tam w ogóle nie być na rysunku
@Rafka odcinka SF mogłoby tam w ogóle nie być na rysunku
