szereg geometryczny, znajdowanie pierwiastków sapensiontko: To zadanie mnie rozłożyło... pomoże ktoś? o funkcji g wiadomo,ze g(x)+g²(x)+g³(x)+...=x gdzie lewa strona równania jest sumą szeregu geometrycznego zbieżnego. Dla jakich wartości parametru m rownanie |g(x)|=2m²−m³ posiada dwa rozwiązania?

a7:

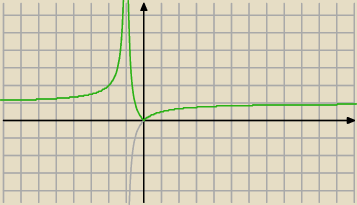
	g(x)		x
L=		g(x)=x−xg(x) czyli g(x)+xg(x)=x czyli g(x)=
	1−g(x)		1+x

	x
|		|=2m2−m3
	1+x

	x
|		|=m2(2−m)
	1+x

m²(2−m)>1

	1−√5		1+√5
czyli m ∊(−∞,		)∪(1,		)
	2		2

a7: jeszcze trzeba dodać te emy kiedy m²(2−m) jest większe od zera a mniejsze od 1

a7: ostatecznie mi wyszło

	1+√5		1−√5
m∊(−∞,		)\{		,0,1}
	2		2

?

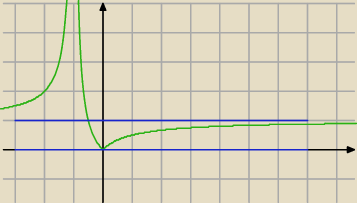
a7: zapomniałam o założeniu −1<g(x)<1 czyli 0<m²(2−m)<1 czyli

	1−√5
m∊(		; 0) ∪ (0,1)
	2

w każdym bądź razie nawet jak się pomyliłam w obliczeniach to metoda jest ok

ite😷: a7 z założenia −1<g(x)<1 chyba wynika warunek dla argumentu a nie bezpośrednio dla parametru?

	x
−1<g(x)<1 oraz g(x)=
	x+1

	x
więc −1<		<1
	x+1

Przecież może się okazać, że g(x) nie przyjmuje jakichś wartości, a f(x)=2m²−m³ może je przyjąć.

a7:

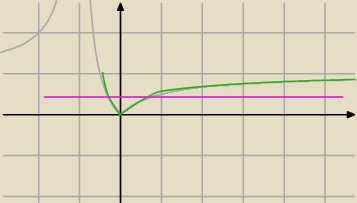
	1−√5
no nie rozumiem? wg moich wyliczeń dla m∊(		, 0) ∪ (0,1) będą dwa punkty przecięcia
	2

ite😷: Zastanowiłam się na zapisem z 8:51, bo chodziło mi o sposób liczenia, nie tylko o sam wynik. Przy tych danych warunek, który otrzymałaś zawiera się w tym z 9:36. Miałam wątpliwości, czy założenie dla funkcji można zastapić założeniem dla parametru.

sapensiontko: Wiem,że pewnie to jest trywialne ale skąd się wzięło:

	g(x)
L=		g(x)=x−xg(x)
	1−g(x)

Widzę tam wzór na sumę szeregu ale nie potrafię tego rozpykać...

a7: przyrównujemy obie strony i wymnażamy x przez mianownik

sapensiontko: aaaa.... mam, po prostu po ułamku jest "wieksza spacja" ja przyjąłem,że to jedno równanie

a7: