obliczanie granicy ciągów
załamany: Kochani, potrzebuję pomocy:
Jak obliczyć granicę właściwą ciągów:
a
n=tg(nπ)
a
n=cos(nπ)
Poproszę o jakieś wskazówki. Samo narysowanie nic mi nie mówi.
15 mar 00:14
15 mar 00:33
a7:
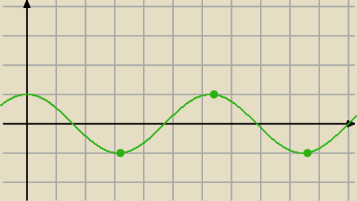
tutaj nie wiem, bo a
1=−1 a
2=1 a
3=−1 a
4=1 ........
15 mar 00:35
załamany: Niczym napisałem to przeczytałem tamtą informację. Tam nie ma nic o granicy ciągów
trygonometrycznych. Jest napisane ogólnie. Chyba jest późno i nie myślę racjonalnie. Według
odpowiedzi ten ma granicę. Swoją drogą w otoczeniu punktu kπ jest "mniej" wyrazów niż ma ten
ciąg. Poprawcie gdzie jeśli się mylę − ta granica to miejsce zerowe?
Ten z cos nie ma granicy właściwej. Odpowiedzi znam z tym, że mam problem ze zrozumieniem czemu
tak jest.
15 mar 00:45
a7: jaką informację przeczytałeś? w linku, no ok tam jest definicja ogólna, ja się dokładnie nie
znam, ale jak bym miała strzelać to wyrazy pierwszsego ciągu przyjmują stale wartość zero i
dlatego jest to granica właściwa, ale to tak w uproszczeniu (nie musi to być miejsce zerowe)
natomiast wnioskuję, że skoro ancosnπ nie ma granicy właściwej, to znaczy, że skoro ciąg
przyjmuje tylko te wartości, to jednak nie można żadnej z nich uznać za granicę właściwą jest
jednak pewnie ograniczony z góry i z dołu
15 mar 00:51
załamany: Z linku, który podałaś.
Generalnie rzecz ujmując mam z tym problem by logicznie to rozumieć. Obie te funkcje są
okresowe; funkcja cosinus jest ograniczona z góry i z dołu, wiec tak jak wskazujesz ma kres
górny i dolny. Chyba musze się z tym przespać. Ale z góry dzięki za chęć pomocy.
15 mar 01:04
a7: już chyba rozumiem w czym masz problem,
funkcja funkcją, a ciąg ciągiem i ja już znajdziesz jego wyrazy to to już zaczyna jakby żyć
własnym (matematycznym) życiem i to już inna bajka
obliczasz wyrazy ciągu wychodzi Ci 0, 0, 0, 0 0 0 0 00 itd. i traktujesz to już niezależnie
od funkcji wyjściowej
w przypadku cosinusa tak samo wyrazy ciągu to 1, −1, 1, −1, itd i już nie patrzysz jakie
własności ma cosinus tylko jakie własności ma Twój ciąg
15 mar 01:08
a7:
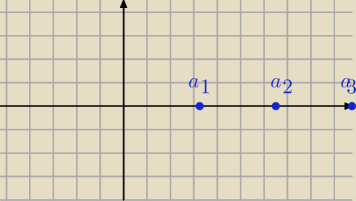
an=tgnπ
15 mar 01:10
a7:
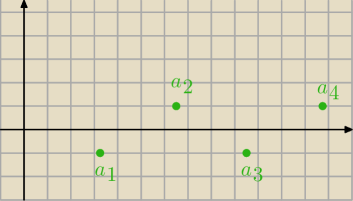
a
n=cos(nπ)
15 mar 01:12
załamany: Ok, ogarnąłem
Dziękuję
15 mar 01:12
a7:
15 mar 01:16
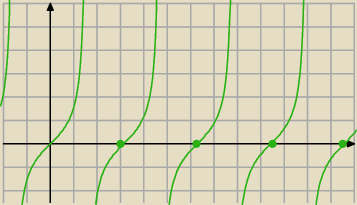a1=tgπ=0 a2=tg2π=0 a3=tg3π=0 .........a7=tg7π=0................