| α | ||
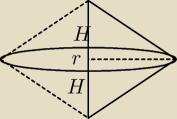
rstożków = hprostokąta = 6sin( | ) | |
| 2 |
| α | ||
2H = podstawa trójkąta = 2*6*cos( | ) | |
| 2 |
| 1 | 2*63 | |||
V(α) = | πr2*(2H) = | cos(a/2)*sin2(a/2) = | ||
| 3 | 3 |
| 2*63 | ||
= | cos(a/2)*(1 − cos2(a/2)) | |
| 3 |
 i jest to dla cosα = ...
i jest to dla cosα = ... 
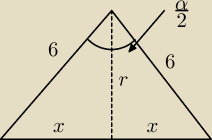 cos(α/2)=r/6 czyli r=6cos(α/2)
x=√62−62cos2(α/2)=6sin(α/2)
V=2V1=2*1/3*π62cos2(α/2)*6sin(α/2)=144πcos2(α/2)*sin(α/2)
https://www.wolframalpha.com/input/?i=y%3D144*%CF%80*cos%5E2%28%CE%B1%2F2%29*sin%28%CE%B1%2F2%29
Vmax=32√3
cos(α/2)=r/6 czyli r=6cos(α/2)
x=√62−62cos2(α/2)=6sin(α/2)
V=2V1=2*1/3*π62cos2(α/2)*6sin(α/2)=144πcos2(α/2)*sin(α/2)
https://www.wolframalpha.com/input/?i=y%3D144*%CF%80*cos%5E2%28%CE%B1%2F2%29*sin%28%CE%B1%2F2%29
Vmax=32√3
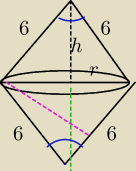 r=p(62−h2}=√36−h2
V=2*1/3*π(36−h2)*h
https://www.wolframalpha.com/input/?i=y%3D2%2F3*pi*%2836-x%5E2%29*x
r=p(62−h2}=√36−h2
V=2*1/3*π(36−h2)*h
https://www.wolframalpha.com/input/?i=y%3D2%2F3*pi*%2836-x%5E2%29*x
| 2 | ||
V'(h)=24π−3h2* | π czyli h=±2√3 | |
| 3 |
| 1 | ||
cosα=√1−sin2α= | ||
| 3 |
 , bo tym sposobem z cosinusami i sinusami połówek kąta α to właściwie nie wyszło bez
Wolframa
, bo tym sposobem z cosinusami i sinusami połówek kąta α to właściwie nie wyszło bez
Wolframa