planimetria w8floosh: Wysokość CD trójkąta równoramiennego ABC, w którym |AC|=|BC|, ma długość h. Na wysokości CD,

	|CE|
jako na średnicy, zakreślono okrąg przecinający ramię BC w takim punkcie E, że		=
	|EB|

	k
		.Oblicz pola trójkątów ABC i CDE
	l

Bleee: Zrób rysunek i skorzystaj z poniższego twierdzenia: https://matematykaszkolna.pl/strona/4004.html

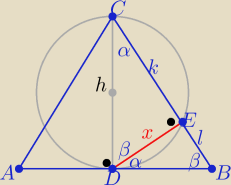
Eta: CD −− jest średnicą to ΔDEC jest prostokątny Z podobieństwa trójkątów DBE i DEC

x		l
	=		⇒x2=kl ⇒ x=√kl
k		x

	1
P(DEC)=		*k*√kl
	2

	k√kl
P(DEC)=
	2

=============== P(ABC) = 2P(DBC) P(ABC)=x*(k+l) P(ABC)=√kl(k+l) ==============

w8floosh: @Eta wszystko byłoby dobrze, ale CE=/=k oraz EB=/=l

w8floosh: proszę o pomoc.

Eta: O co Ci chodzi? bo nie rozumiem?

w8floosh: chodzi o to, że odcinki CE i EB są w stosunku k do l, a w twoim rozwiązaniu założyłaś że CE=k i EB=l.

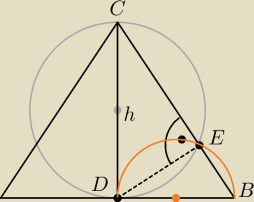
wredulus_pospolitus: Tak jak na samym początku napisałem −−− skorzystaj z odpowiedniego twierdzenia (podane w pierwszym moim poście).

|CE|		k
	=		−> |CE| = k*a ∧ |EB| = l*a
|EB|		l

	h2
h2 = |CB|*|CE| = (k+l)*k*a2 −−−> a2 =
	(k+l)k

	l
|DB|2 = |CB|*|EB| = (k+l)*l*a2 −−−> |DB|2 = h2*
	k

P(ABC) = |DB|*h = h⁴*√l/k

wredulus_pospolitus: dobra −−− spitoliłem trochę P(ABC) = |DB|*h = h²*√l/k oczywiście

w8floosh: Dziękuję, ale skąd wzięła się równość |DB|2 = |CB|*|EB| oraz jak wygląda sytuacja z polem trójkąta CDE?

wredulus_pospolitus: 1) Spójrz do linka podrzuconego na samym początku tematu. Z tego twierdzenia skorzystałem dwukrotnie: I. odcinek |CD| = h jest styczny do okręgu II. odcinek |BD} jest styczny do okręgu

wredulus_pospolitus:

	1
P(CDE) + P(DBE) =		P(ABC)
	2

z podobieństwa trójkątów (skala):

P(DBE)		|DB|		(k+l)l*a2		l
	= (		)2 =		=
P(CDE)		h		(k+l)k*a2		k

	l
−−−> P(DBE) =		P(CDE)
	k

więc: P(CDE) = ....

Eta:

	ka		k
Bez straty ogólności :		=		bo a≠0
	la		l

Cz teraz jasne?

wredulus_pospolitus: Etuś ... problem w tym, że w Twojej postaci masz wtedy: P(ABC) = √kl(k+l)*a³ którego nie znamy ... więc musimy go wyznaczyć w zależności od h

wredulus_pospolitus: I oto chodziło autorowi pisząc 20:51

Eta: Od kiedy to √kl(k+l) daje a³ ? √kala= a√kl*a(k+l) i mamy a²(.....)

wredulus_pospolitus: racja a² ... co nie zmienia faktu, że tenże a² trzeba wyrazić teraz za pomocą (np. h²)

Eta: Jak dla mnie..... to za dużo danych ( h −−− zbędne) wystarczy k i l Ja podałam rozwiązanie zależne tylko od k i l

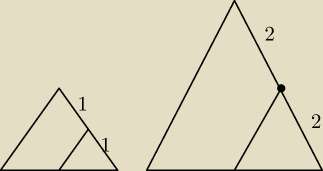
wredulus_pospolitus: k i l to tylko proporcja Nie ... nie podałaś rozwiązania zależnego od k i l Bo w Twoim rozwiązaniu Otrzymamy dla |CE| = 1 i |EB| = 1 P(ABC) = √kl(k+l) = 1*2 = 2 A dla |CE| = 2 i |EB| = 2 P(ABC) = 1*2 = 2 h −−− to jest jedyna wartość która przedstawia nam jakąkolwiek długość w tym trójkącie i musimy się na niej opierać aby

wredulus_pospolitus: (pomijając kwestię tego że wziąłem nierealną proporcję podziału długości tego boku do warunków zadania)