W trójkącie prostokątnym o przyprostokątnych a i b kąt leżący naprzeciwko przypr madzia03: W trójkącie prostokątnym o przyprostokątnych a i b kąt leżący naprzeciwko przyprostokątnej b ma miarę β oraz cosβ=√2/5 Oblicz wartosc wyrażenia ^a_a+b − ^b2_a²−b²

Szkolniak: przeciwprostokątna trójkąta: c=√a²+b²

	√2
cosβ=
	5

	a
cosβ=
	√a2+b2

	√46
stąd: 5a=√2(a2+b2) ⇒b=
	2

teraz podstawić w wyrażeniu pod b

Szkolniak:

	√46
umknęło mi: b=		a
	2

Mila:

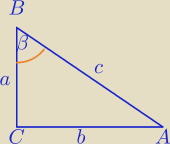
	√2		a
cosβ=		=
	5		c

	b		√23
sinβ=		=
	c		5

	a		b2
w=		−		=
	a+b		a2−b2

	a*(a−b)−b2		a2−b2−ab
=		=		=
	(a2−b2)		a2−b2

	ab		a   b   * c   c
=1−		=1−		=
	a2−b2		a2   b2   − c2   c2

	√2   √23   * 5   5
=1−		=
	4   23   − 25   25

	√46
=1+
	19

Eta:

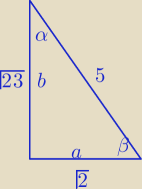
	√2		23		√2(√23−√2)+23		√46+21
W=		+		=		=
	√23+√2		23−2		21		21

	√46
W=1+
	21

==========