stereometria salamandra: Pole przekroju osiowego stożka jest π√3 razy mniejsze od pola powierzchni całkowitej. Wyznacz miarę kąta zawartego między tworzącą, a wysokością tego stożka

	2r*H
P przekroju:		= r*H
	2

P_c=πr(r+l) H=√l²−r²

πr(r+l)
	=r*√l2−r2
π√3

r2+rl
	=r*√l2−r2
√3

r²+rl=r*√3l²−3r² r(r+l)=r*√3l²−3r² r+l=√3l²−3r² / 2 r²+2rl+l²=3l²−3r² 2rl=2l²−4r² / : 2 rl=l²−2r² zwykle w zadaniach tego typu coś trzeba bylo od czegos uzależnić, a tutaj kompletnie mi nic nie wychodzi, na różne sposoby już próbowałem

Mila: π√3*r*H=πr²+πr*l √3*H=r+l /:l

	H		r
√3*		=		+1
	l		l

√3*cosα=sinα+1 dokończ

salamandra: wow, aż równanie jakieś z tego powstało? zaraz spróbuję

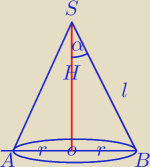
Mila: Patrz na rysunek i wyciągaj wnioski. Napisałam więcej, ale przypomniałam sobie, że zrobiłeś ostatnio duże postępy, to wymazałam cd.

salamandra: Nie no, ja widzę skąd to wzięłaś, ale sam bym na takie coś aż nie wpadł √3*cosα=sinα+1 √3*cosα−sinα=1

	√3		1
2(		*cosα−		*sinα)=1
	2		2

2(sin60*cosα−cos60*sinα)=1

	1
sin60*cosα−cos60*sinα=
	2

	1
sin(60−α)=
	2

	π		1
sin(		−α)=
	3		2

π		π		π		5
	−α=		+2kπ v		−α=		π+2kπ
3		6		3		6

π		π		−3π
	−		−2kπ=α v		−2kπ=α
3		6		6

π		−π
	−2kπ=α v		−2kπ=α
6		2

α=30 stopni

salamandra:

	1
w sumie to głupi jestem, po co to rozwiązywałem jak to od razu widać, że sin(60−α)=		,
	2

więc α = 30.....

Mila: Trzeba było napisać, że α− kąt ostry. Dobrze.