Geometrii analityczna Natalia: Dany jest okrąg o równaniu x²+y²+4x−6y+9=0 Napisz równania stycznych do tego okręgu przechodzących przez początek układu współrzędnych

Leszek: Niech y = ax , podstaw do rownania okregu i wes warunek Δ = 0

piotr: x²+(ax)²+4x−6ax+9=0 Δ=−4 (12 a + 5) Przyrównując Δ=0 ⇒ a = −5/12 styczna: y = −5x/12 ale stycznych musi być dwie: dochodzi styczna x=0

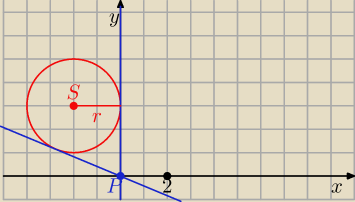
janek191: Inny sposób: ( x + 2)² − 4 + ( y − 3)² − 9 + 9 = 0 ( x + 2)² + ( y − 3)² = 2² S = ( − 2, 3) r = 2 y = a x + b P = ( 0,0) b = 0 a x − y = 0 Odległość tej prostej od S jest równa 2, więc

I −2 a − 1*3 I
	=2
√a2 + 1

I −2 a − 3I = 2 √a² + 1 −2 a − 3 = 2 √a² + 1 4 a² + 12a + 9 = 4 a² + 4 12a = − 5

	5
a = −
	12

	5
y = −		x lub x = 0
	12

========================

daras: to już chyba było ze 1000x wałkowane na tym forum?

Eta: Janek chce być 101

daras: chyba 1002?