Rozwiąż równanie czarniecki: Rozwiąż równanie: x=^{(5√3+5)*sin60}_sin75 a²=x²+(^5√3+5₂)²−2*x*^5√3+5₂*cos 45 Wyszło mi √^200−25√3₂, ale to nie zgadza sie z odpowiedzią, wiec gdzieś muszę mieć błąd

wredulus_pospolitus: A możesz podać skąd takie równanie z tw. cosinusów

czarniecki: Trójkąt ABC obracamy wokół prostej zawierającej bok AB. AB=5(√3+1), kąt przy a=60, kąt przy b=45. Czy na tej bryle można opisać kulę? Skoro obrót jest wokół AB, to AB musi być średnicą, a więc promień równa się ^5(√3+1₂. Żeby dało się na tej bryle opisać kule, to odległość od środka AB, do wierzchołka C, musi równać się promieniowi. Z tw. sinusów, wyznaczam bok BC, a następnie wstawiam go do tw. cosinusów, z połową promienia. Zależy mi na TYM ROZWIĄZANIU, a nie tym z wysokościami trójkąta, które można znaleźć na internecie.

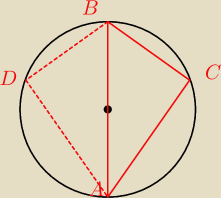
wredulus_pospolitus: Po co Ci to wszystko 1) Zauważ, że już deltoid ACBD nie spełnia warunku koniecznego do tego, że na nim można opisać okrąg (suma kątów przeciwległych = 180^o) 2) Mogłeś też to zauważ w momencie: ∡ACB = 75^o ... związku z tym okrąg opisany na trójkącie ABC NIE MA środka w środku AB (tak jak to sugeruje powyższy rysunek), ponieważ to jest prawdą tylko dla trójkąta prostokątnego, a ten takim nie jest. Skoro na czworokącie nie można opisać okręgu, to na powyższej bryle nie można opisać sfery/kuli, której przekrojem byłby właśnie tenże okrąg.

czarniecki: Dzięki wielkie, kompletnie o tym nie pomyślałem

czarniecki: Ale z ciekawości, sprawdzisz czy dobrze rozwiązałem te równania?

Bleee: Nie bo przy liczeniu promienia przyjąłeś coś co nie jest prawda Nic dziwnego że później się wszystko 'haczy'

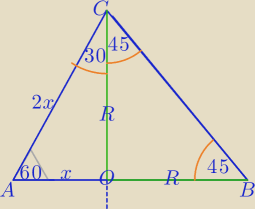
Mila: x+R=5*(√3+1) R=x√3 x+x√3=5*(√3+1) x*(1+√3)=5*(√3+1) x=5 R=5√3 Nie wiem co masz obliczyć, ale masz już wszystko.