Planimetria Kaja: Punkt E dzieli bok AB trójkąta ABC w stosunku |AE|EB|=3/8 . Odcinek CE przecina środkową tego trójkąta AF w punkcie S . Oblicz |SE|CS|

Kaja: |AE| : |EB| = 3/8 * Oblicz |SE| : |CS|

Kaja: nie mam pojęcia jak się za to zabrać

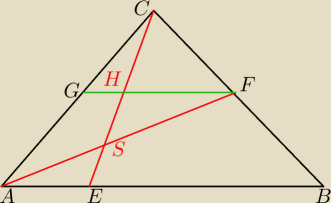
an: 3/11 popatrz na trójkąty SHF i SEA

Mila:

|AE|		3
	=
|EB|		8

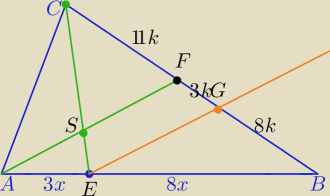
1) EG||AF Z tw. Talesa : ramiona kata ABF przecięte prostymi równoległymi AF i EG

FG		GB		FG		GB
	=		⇔		=
AE		EB		3x		8x

FG		3
	=
GB		8

|FG|=3k i |GB|=8k, gdzie k− wspólna miara ⇒|CF|=11k 2) Ramiona kąta ECG przecięte prostymi równoległymi j.w⇔

SE		CS		SE		CS
	=		⇔		=
FG		CF		3k		11k

SE		3
	=
CS		11

=============

an: Proponuję przy okazji zmianę pieluszek

Karimata: To zmień swojemu niemowlakowi, zamiast siedzieć na forum.

anonim: a ja się cieszę, że jest Ktoś (a nawet kilka takich "Ktosiów") na tym forum, kto podaje rozwiązania, z których można coś zrozumieć i jeszcze sprawdzić wynik i jeszcze się w razie czego dopytać, rozumiem, że innym się nie chce rozwiązywać dla innych i chyba uważają, że wszyscy sami powinni tak samo dobrze rozumieć matematykę jak oni, ale jeszcze uszczypliwości innym sadzić to lekka przesada