stereometria
Patryk: W kulę wpisano dwa stożki o wspólnej podstawie, przy czym jeden z nich ma pole powierzchni
bocznej trzy razy większe niż drugi. Oblicz stosunek długości wysokości tych stożków.
| | 1 | |
Zadanie zrobiłem, ale nie zgadza sie moja odpowiedź z odpowiedzią w książce (k = |
| ), mi |
| | 9 | |
wyszło 3.
l
1 − tworząca większego stozka
l
2 − tworząca mniejszego
Pb1 = 3*Pb2
πrl = 3πrl
2
l = 3l
2
h
12 + r
2 = (3l
2)
2
h
12 = 9l
22 − r
2
h
22 = l
22 − r
2
k = 3
Może to przez to, że powinienem mieć jedną zmienną przy dzieleniu tylko? Nie uzależniałem w
prawdzie danych od jednej nie wiadomowej a może powinienem
10 mar 23:48
Eta:
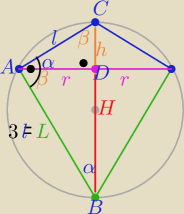
Z treści zadania L=3l
Z podobieństwa trójkątów ADC i ADB w skali k=1/3
| | P(ADC) | | r*h | |
to |
| = |
| =k2 |
| | P(ADB) | | r*H | |
===============
i po ptokach
11 mar 00:40
wredulus_pospolitus:
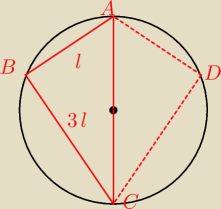
Zauważ, że ΔABC jest wpisany w okrąg (przekrój kuli).
związku z tym, ∡ABC = 90
o
więc h
1 + h
2 =
√10l
h
12 = 9l
2 − r
2
h
22 = l
2 − r
2
h
12 − h
22 = 8l
2
(h
1 + h
2)(h
1 − h
2) = 8l
2
√10l * (h
1 − h
2) = 8l
2 −> h
1 − h
2 = ...
znasz sumę dwóch ... znasz ich różnicę ... wyznacz jedną i drugą wysokość
11 mar 00:40
Eta:
Ale się "wredulus" opisałeś
( choć jesteś podobno "leniwy"
11 mar 00:43
wredulus_pospolitus:
bo nie podzieliłem tego deltoidu i nie zauważyłem trójkątów podobnych
11 mar 00:44
Eta:
W tym sęk
Zadanie każdy rozwiązać może
ale najkrótszą drogą ..... tylko nieliczni mogą !
11 mar 00:47
Patryk: Dziękuję
11 mar 09:50