Zbiór wartości funkcji z szeregiem geometrycznym FUITP: Cześć, mam takie zadanie:

	x		x		x
Wyznacz zbiór wartości funkcji f(x) =		+		+		+ ..., jeżeli
	x−2		(x−2)2		(x−2)3

	x		x		x
wyrażenie		+		+		+ ... jest szeregiem geometrycznym.
	x−2		(x−2)2		(x−2)3

Zrobiłem założenia:

	1
q =
	x−2

	x
−1 <		< 1
	x−2

x∊ (−∞ ; 1) ∪ (3 ; +∞)

	x		3		3
Suma szeregu to:		=		+ 1 ⇒ f(x) =		+ 1
	x−3		x−3		x−3

I teraz w odpowiedziach zbiór wartości to (−¹₂; 1) ∪ (1; +∞). Te jedynkę rozumiem bo to asymptota pozioma, ale skąd to −¹₂?

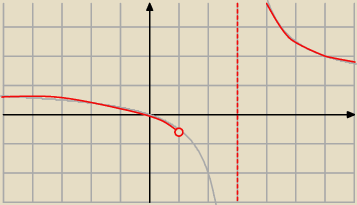wredulus_pospolitus: a jaką masz dziedzinę funkcji

jc:

	1
−1 <		< 1
	x−2

x>2 lub x<1

FUITP: O racja. Kompletnie nie zwróciłem na to uwagi. Dziękuję.

wredulus_pospolitus: jc ... jednak x>3 dla x = 2.5 wyskoczysz poza przedział (−1 ; 1)

jc: Jasne, że x>3