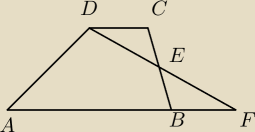
 W trapezie ABCD punkt E jest srodkiem boku BC oraz |AB| = 2|CD|. Z wierzchołka D
poprowadzono prosta przecinajaca bok BC w punkcie E. Proste AB i DE przecinaja sie w
punkcie F (zobacz rysunek)
W trapezie ABCD punkt E jest srodkiem boku BC oraz |AB| = 2|CD|. Z wierzchołka D
poprowadzono prosta przecinajaca bok BC w punkcie E. Proste AB i DE przecinaja sie w
punkcie F (zobacz rysunek)
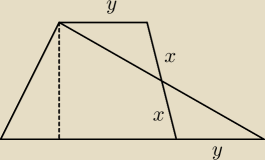 to Ci daje fakt, że to są takie same trójkąty
to Ci daje fakt, że to są takie same trójkąty
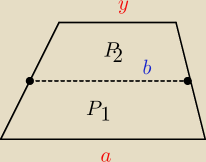 P1 + P2 = Ptrapezu
wiemy, że a = 2y
P1 + P2 = Ptrapezu
wiemy, że a = 2y
| a+y | 3 | |||
b = | = | y | ||
| 2 | 2 |
| 7 | ||
P1 = | y*h | |
| 4 |
| 5 | ||
P2 = | y*h | |
| 4 |
| yh | ||
PΔBFE = PΔCDE = | ||
| 2 |
| 5 | ||
PABED = Ptrapezu − PΔCDE = | yh | |
| 2 |
 yhh
yhh
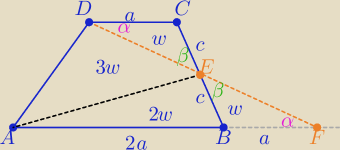 1/ rysunek
2/ ΔDFE≡ΔDEC z cechy (kbk) to P(BFE)=P(DEC)=w
3/ P(ABE)=2p(BFE)=2w
4/ AE jest środkową ΔAFD zatem P(AED)=3w
P(ABED)=5w P(BEF)=w
1/ rysunek
2/ ΔDFE≡ΔDEC z cechy (kbk) to P(BFE)=P(DEC)=w
3/ P(ABE)=2p(BFE)=2w
4/ AE jest środkową ΔAFD zatem P(AED)=3w
P(ABED)=5w P(BEF)=w
| 1 | ||
P(BEF)= | P(ABED) | |
| 5 |