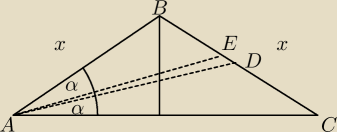
 W trójkącie równoramiennym ABC ( |BA| = |BC| , punkt E należy do boku BC i do dwusiecznej kąta
BAC, natomiast AD jest środkową w tym trójkącie. Oblicz pole trójkąta ADE wiedząc, że |AC| = 6
oraz |∡ACB| = 30o.
W trójkącie równoramiennym ABC ( |BA| = |BC| , punkt E należy do boku BC i do dwusiecznej kąta
BAC, natomiast AD jest środkową w tym trójkącie. Oblicz pole trójkąta ADE wiedząc, że |AC| = 6
oraz |∡ACB| = 30o.
| 1 | ||
2) PΔABC= | *6*√3=3√3 | |
| 2 |
| 3√3 | ||
PΔACD= | =PΔABD | |
| 2 |
| x | AC | ||
= | |||
| BE | CE |
| 2√3 | 6 | ||
= | |||
| BE | 2√3−BE |
| 6 | ||
|BE|= | ||
| 3+√3 |
| 1 | ||
4) Oblicz pole ΔABE: PABE= | *x*|BE|*sin 120o | |
| 2 |