Zadanie bASIA: krawędź podstawy prawidłowego ostrosłupa czworokątnego ma długość 6cm. Kąt który tworzy krawędź boczna z wysokością ostrosłupa ma miarę 30 stopni. Przez wierzchołek ostrosłupa poprowadzono płaszczyznę prostopadłą do przeciwległej krawędzi bocznej. Oblicz pole otrzymanego przekroju.

Rudy: Coś nie tak z treścią wg. mnie Płaszczyzna prostopadła do krawędzi bocznej, przechodząca przez wierzchołek ostrosłupa nie tworzy przekroju, ma jeden punkt wspólny z krawędzią − wierzchołek ostrosłupa. Sprawdź treść.

bASIA: nio tresc jest dobra

bASIA: i to ma wyjsc deltoid

bASIA: prosze o pomoc

Kuba: treść jest dobra tylko jako wierzchołek trzeba przyjąć 'wierzchołek podstawy'

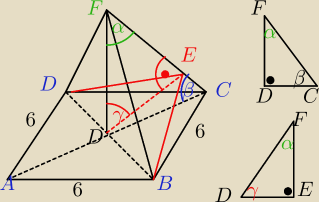
tyu: Krawędź podstawy prawidłowego ostrosłupa czworokątnego ma długość 6 cm. Kąt, który tworzy

	π
krawędź boczna z wysokością ostrosłupa ma miarę		. Przez wierzchołek ostrosłupa
	6

(podstawy ostrosłupa) poprowadzono płaszczyznę prostopadłą do przeciwległej krawędzi bocznej. Oblicz pole otrzymanego przekroju. prawidłowa odpowiedź to 12√3. Mi niestety wychodzi 9√3 α=30 β=60 γ=60 moje obliczenia AC= 6√2 DC=3√2

	FD
z Δ FDC liczę FD, więc tg60=		FD=3√6
	3√2

	DE		3√6
z ΔFDE liczę DE, więc sin30=		DE=
	3√6		2

	3√6
No i wychodzi pole P=0,5*6√2*		=9√3
	2

czy ktoś widzi błąd

Piotr 10: A patrzyłeś w necie na rozwiązania może ?

tyu: patrzyłem. Jest jedno tu http://www.matematyka.pl/178905.htm , ale załączony obrazek − podpowiedź − został wykasowany, więc ciężko coś z tego zrozumieć W moim obrazku jest błąd. wierzchołek podstawy i punkt przecięcie się przekątnych są tak samo oznaczone, to jest literą D.

Piotr 10: Tutaj masz ładny rysunek http://forum.zadania.info/viewtopic.php?f=21&t=7228 Ten przekrój to deltoid musi być

tyu: aha, to zupełnie inaczej wygląda. Dziękuję Piotr 10 Zabieram się do przeanalizowania rozwiązania.