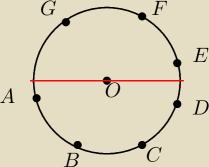
kombinatoryka salamandra: Na okręgu o środku O zaznaczono punkty od A do G. Oblicz ile cięciw których końcami są 2 z zaznaczonych punktów: a) przetnie średnicę KL, b) nie przetnie średnicy KL zacząłem od podpunktu b)

4 2
	=6

3 2
	=3

6+3=9

	7 2		7!		7*6*5!		42
a)		=		=		=		=21
			2!*5!		2!*5!		2

21−9=12 I w ten sposób rozumiem jak zrobiłem, natomiast w odpowiedzi jest do a) 3*4 lub 4*3 i nie wiem jak to czytać, tak to rozumiem metodę mnożenia, ale tutaj nie wiem co się z czym łączy

Jerzy: a) czy np. cięciwa AD przecina tą średnicę ?

wredulus_pospolitus: (a) wybierasz jeden z punktów 'poniżej' cięciwy (4 sposoby) i jeden z 'powyżej' cięciwy (3 sposoby) stąd 4*3 = 12

Jerzy: A, nie zauważyłem, że odjąłeś.

salamandra: dzięki

Mila: a) Zostanie przecięta cięciwa KL , jeżeli połączymy Punkty A,B,C,D z punktami E,F,G Możemy to zrobić na : 4*3 sposoby −Każdy " dolny " punkt wybieramy na 4 sposoby a górny na 3 sposoby albo odwrotnie. Na tyle sposobów możemy połączyć w pary dolne punkty z górnymi. Twój sposób też jest dobry.

salamandra: Teraz już jasne − chwilowe zaćmienie miałem

salamandra: A tutaj: Oblicz ile jest wszystkich liczb naturalnych trzycyfrowych takich, że w ich zapisie dziesiętnym: a) występują tlyko cyfry nieparzyste lub tylko cyfry parzyste b) występuje jedna cyfra nieparzysta i dwie parzyste c) wystepuje jedna cyfra parzysta i dwie nieparzyste a) nieparzyste: 5*5*5=125 parzyste: 4*5*5=100 125+100=225 b) parzysta na początku i w jakimś innym miejscu 4*5*5=100 parzysta w innym miejscu niż pierwsze 5*5*5=125 125+100=225 i nie rozumiem, czemu trzeba rozpatrzyć przypadki, gdzie parzysta stoi na drugim i na trzecim oddzielnie, przecież to nie ma znaczenia, znaczenie ma tylko wtedy, gdy stoi na pierwszym, bo tam nie może być zero?

Jerzy: Dokładnie tak. Nie ma znaczenia czy stoi na drugim ,czy trzecim,bo i tak jest to 5*5

salamandra: No więc według mnie powinno to być 225, a jest 325

salamandra: nie rozumiem dlaczego trzeba rozpatrywac przypadki: 1) parzysta na poczatku 2) parzysta w srodku 3) parzysta na koncu a nie tylko 1) parzysta na poczatku 2) parzysta gdzieś indziej

Jerzy: Głupotę napisałem: pnp i ppn , to dwie różne liczby.

salamandra: no tak, ale ja to rozumuję w ten sposób 1) parzysta na poczatku 1−sza na 4 sposoby, druga na 5, trzecia na 5 2) parzysta na innym miejscu 1−sza na 5 sposobów, druga na 5 i trzecia również na 5.

Jerzy: ppn + pnp = 2*4*5*5

Bleee: Ale rozpatrując (1) musisz rozpatrzeć przypadek: pnp oraz ppn a ty tak zapisując rozpatrujesz tylko jeden z nich Tutaj (2) natomiast rozpatruje prawidłowo sytuację npp i koniec.

Mila: {0,2,4,6,8} {1,3,5,7,9} W przypadku b) NPP lub ( PNP lub PPN tu wybierasz na 2 i 3 pozycje z innych zbiorów) 5*5*5 lub 4*5*5 lub 4*5*5 czyli 5*5*5+2*(4*5*5)= 125+2*100=325 ============== Wszystkich 3−cyfrowych liczb masz 900 i suma przypadków: PPP, NNN, PNP, PPN, NPP,PNN, NPN, NNP musi dać 900

salamandra: dzieki