Planimetria kąty Frajvald: Witam mógłby ktoś pomóc z czymś takim? W trójkącie ostrokątnym ABC poprowadzono wysokości BD i CE. Wykaż, że kąt ABC + kąt BDE = 90. próbowałem coś z okręgiem opisanym i trójkątami podobnymi ale nic mi nie chce wyjść.

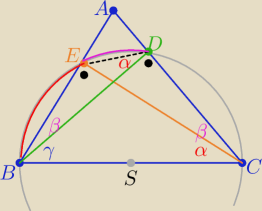
a@b: Dodaj odpowiednie komentarze ( do rysunku i masz tezę ∡ABC+∡BDE =γ+β+α=90^o

Frajvald: Dzięki wielkie, nie spojrzałem na to w ten sposób

a@b:

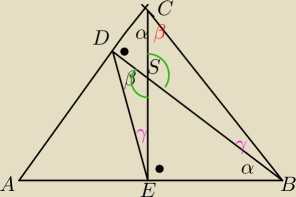
a7: https://matematykaszkolna.pl/forum/27878.html korzystam z uzasadnienia wlinku, że kąt ABD=kątACE kątCAE=90−α KątCSD=kątESB=90−α kąt CDE=180−90−α−β=90−α−β kąt DSE=kąt CSB=90+α mamy udowodnić że α+γ+β=90 trójkątyEDB i CBS są podobne (?), więc kąt EBD+kątEDB+90+kątDES=180 czyli α+β+γ=90 ?

a@b: To było 11 lat temu ( już zapomniałam ,że tak rozwiązywałam No to Frajvald ma dwa sposoby