Stereometria
Kasia18: Graniastosłup prawidłowy czworokątny ABCDA'B'C'D' przecięto płaszczyzną (ACQP) , przy czym
punkty P i Q należą do krawędzi odpowiednio A'B' i B'C' . Krawędź podstawy tego graniastosłupa
ma długość 4 , jego wysokość długość 12 , a płaszczyna nachylona jest do podstawy
graniastosłupa pod kątem 6√2 .
Oblicz wysokość trapezu otrzymanego w przekroju.
Bardzo proszę o pomoc,
8 mar 20:20
Tadeusz:
pod kątem 6√2 ... powiadasz ...
8 mar 20:55
Kasia18: tan(a)=6√2
przepraszam
8 mar 21:08
a7:
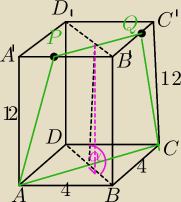
tgα=sinα/cosα sinα=12/h cosα=x/h
tgα=6
√2=12/h*(h/x) czyli x=
√2
h
2=x
2+12
2 czyli h=
√146
?
8 mar 21:23
Kasia18: Oblicz długośc odcinka PQ
Oblicz pole powierzchni otrzymanego przekroju
Jeszcze 2 polecenia do zadania były
9 mar 00:15
Kasia18: Bardzo proszę o pomoc
9 mar 00:23
a7:
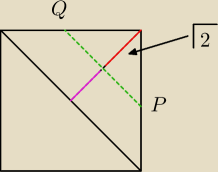
|PQ|=2
√2
| | (4√2+2√2)*√146 | |
PPRZEKROJU= |
| =.... |
| | 2 | |
9 mar 00:32