Dowodowe z planimetrii jokeros2000: Wykaż, że jeżeli długości a,b,c boków trójkąta spełniają równość ¹_a+b+¹_b+c=³_a+b+c to promień okręgu opisanego na tym trójkącie jest równy ^b√3₃ Myślałem, żeby to zadanie ruszyć z twierdzenia sinusów tylko nie wiem do końca jak

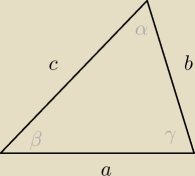
Saizou : Podpowiedź Z podanej równość mamy, że b²=a²+c²−ac z tw. cosinusów mamy, że b²=a²+c²−2accosβ zatem −ac=−2accosβ

	1
cosβ=		→β=60°
	2

jokeros2000: Dzięki bardzo

Patryk: W jaki sposób uprościłeś to równanie? Sprowadzałeś do wspólnego mianownika?

Saizou : pomnóż obustronnie przez iloczyn mianowników i upraszczaj

Patryk: Ok, myślałem, że jest jakaś prostsza metoda

Saizou : ale to jest proste, mnożenie nawiasów nie jest złe