geometria analityczna Gangster:

	2
Punkty A(1, 2) i B(2, 1) leżą na hiperboli o równaniu y =
	x

, gdzie x ≠ 0. Znajdź na tej hiperboli taki punkt C o ujemnej odciętej, aby pole trójkąta ABC było najmniejsze.

	2
Nie wiem jak sie za to zabrac, wiem ze C bedzie mial wspolrzedne (x		) ale co dalej?
	x

podstawiac do wzoru na pole= 1/2|(xb−xa)... ? Jak sie pozbyc wtedy wart bezwzglednej?

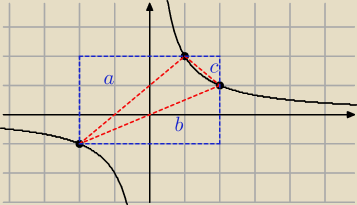
wredulus_pospolitus: pamiętaj, że x < 0 Pole szukanego trójkąta =

	2
Pole prostokąta o bokach: 2+x , 2 +
	x

−

	2
Pole trójkąta o przyprostokątnych: 1+x, 2 +		(a)
	x

−

	2
Pole trójkąta o przyprostokątnych: 2+x, 1 +		(b)
	x

− Pole trójkąta o przyprostokątnych: 1, 1 (c)

Gangster: Wysle pozniej rozwiazania na gg zernknij jak mozesz

wredulus_pospolitus: więc masz:

	4		1		2		4
PΔ = 6 + 2x +		−		[ 4 + 2x +		+ 4 + x +		+ 1 ] = ...
	x		2		x		x

I szukasz minimum tej funkcji (pamiętaj, że x < 0 )

wredulus_pospolitus: mnie nie będzie przez najbliższą godzinę / półtorej

wredulus_pospolitus: fuck .... oczywiście x > 0 we wzorach na pola

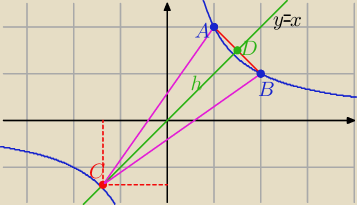
a@b: Można też tak: ( bez pochodnych)

	2
Z symetrii osiowej wykresu f(x)=		względem prostej y=x
	x

to C(x, x) i x<0 z treści zadania ΔABC równoramienny o ramionach AC =BC więc Pole będzie najmniejsze wysokość CD Δ będzie najkrótsza Rozwiązując układ równań: y=x i y= 2/x ⇒ x²=2 i x<0 ⇒ x= −√2 zatem C(−√2, −√2) ========== i po ptokach

Bleee: a@b − − − uzasadnienie że ten trójkąt ma najmniejsze pole

a@b: Co tu uzasadniać ? podałam wyżej Równoramienny , długość podstawy stała AB to dla najkrótszej wysokości pole najmniejsze Najkrótsza wysokość CD , C∊y=x . C(x,x) i x<0 itd. ble ble ble

wredulus_pospolitus: A co gdyby to była inna krzywa bądź inne byłyby punkty A, B Dla A(1,2) i B(4, 0.5) także równoramienny będzie miał najmniejsze pole?

a@b: Mówimy o zadaniu o podanej treści ( a nie o jakieś innej treści)

a@b: Z treści zadania ............ Δ równoramienny! więc o co kaman?

wredulus_pospolitus: o to, że ... nie podałaś argumentacji która jednoznacznie przekazuje nam, że to będzie właśnie trójkąt równoramienny. To, że on będzie w tym zadaniu nie oznacza że to jest pewne i nie należy sprawdzić innych opcji.

wredulus_pospolitus: takie zadanie na maturze na 100% nie uzyska pełnej puli punktów, ponieważ ZAKŁADASZ coś czego nie wiesz (a przynajmniej nie uzasadniasz, że tak właśnie będzie).

Gangster: wredulus zerknij gg

a@b: Ale jesteś "upierdliwy" ! Co zakładam? .... Napisałam 1/prosta y=x jest osią symetrii tak? jasne że tak itd Przeczytaj uważnie co napisałam i dopiero wtedy... podważaj moją argumentację Tyle w temacie !

wredulus_pospolitus:

	2
tak ... y=x jest osią symetrii f(x) =		i co związku z tym
	x

Czy jest to równoznaczne z tym, że najkrótsza odległość będzie leżeć na tej prostej (która zawiera też połowę odcinka AB) Odpowiedź brzmi −−−− NIE

wredulus_pospolitus: To, że dla tej konkretnej funkcji tak będzie ... nie oznacza że prawdą będzie: Jeżeli prostopadła do odcinka leży na osi symetrii funkcji f(x) to najkrótsza odległość punktu na f(x) os tegoż odcinka będzie leżeć na osi symetrii.

a@b: Odpowiedź brzmi : taaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaak bo A(1,2) i B(2,1) są symetryczne względem prostej y=x Zatem...................................... Nie mam już siły do Ciebie

a@b: Czy Ty umiesz czytać co napisałam? W tym zadaniu akurat tak będzie! O innych przypadkach nie piszę, tylko o tym

a@b: 100% na maturze dostałabym jak nic!

wredulus_pospolitus: a@b −−− to że w tym przypadku ta będzie nie oznacza, że Ty jako uczeń piszący maturę możesz napisać: "tutaj tak będzie w tym przypadku, bo ja to wiem" i pierdut dajesz wynik. Gdyby to było zadanie na sprawdzianie to sprawdzający by napisał: "a dlaczego?" ewentualnie "a skąd mamy pewność?" i obciął punkty. Na maturze nie napisze, ale punkty obetnie. Tak jak napisałem −−− to nie jest prawdą dla każdej funkcji f(x) takiej, że jest symetralna względem prostej y = x i nawet weźmy te same punkty A i B. A jeżeli piszesz, że dla tej funkcji tak właśnie jest to .... musisz pokazać z czego to wynika, bądź to udowodnić.

a@b: No comment ... szkoda każdego słowa !