geometria analityczna Gangster: Dane są cztery punkty leżące na płaszczyźnie: A(6, 2), B(8, 4), C(7, 9) oraz D(1, 3). a) Udowodnij, że czworokąt ABCD jest trapezem równoramiennym. b) Napisz równanie okręgu opisanego na tym trapezie. z podpunktem a nie mam problemu, jedynie nie wiem jak zabrac sie za b, symetralne bokow? czy jest moze jakas lepsza metoda?

ite: Symetralne nierównoległych boków , punkt ich przecięcia jest środkiem okręgu opisanego.

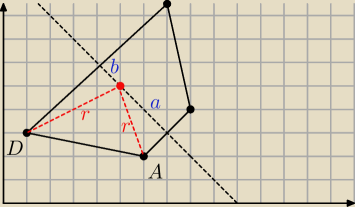
wredulus_pospolitus: nie tyle boków co podstaw symetralna daje Ci prosta na której ma być środek okręgu zauważ, że znasz odległość punktów A i D od symetralnej (a raczej możesz ją wyliczyć) i będzie to odpowiednio √2 i 3√2 więc masz dwie możliwości: 1) (zaprezentowane na rysunku) a² + 2 = r² b² + 18 = r² a+b = 3√2 2) (gdy środek okręgu jest powyżej dłuższej podstawy) a² + 2 = r² b² + 18 = r² a−b = 3√2

Gangster: Wredulus zerknij pozniej jak mozesz na gg, wysle 2/3 zadanka do sprawdzenia