Geometria AHQ: Dany jest trójkąt ostrokątny ABC oraz punkt P leżący na stycznej do okręgu opisanego na ABC w punkcie A. Rzuty punktu P na boki AB i AC tego trójkąta oznaczmy przez F i E. Wykaz, ze prosta EF jest prostopadła do BC.

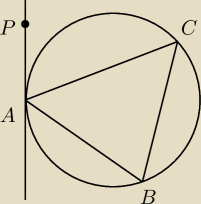
wredulus_pospolitus: wybacz ... ale jak niby ma wyglądać rzut punktu P na bok AB

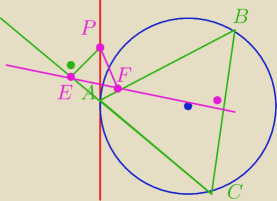
janek191: Może zamiast na boki AB i AC powinno być na proste AB i AC ?

AHQ: Tak, dokładnie. Kolejny raz polecenie niezbyt jasne. Mój błąd

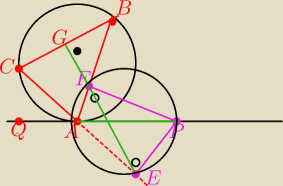
AHQ: Sprawdzi ktoś ? Wykażemy, że ΔGFB jest prostokątny. Niech ∠QAC=α Wtedy również ∠ABC=∠PAE=α Zauważmy, że na AEPF można opisać okrąg. ∠EFP zatem rowny jest α (jest oparty na tym samym łuku co ∠PAE. ∠AFE=∠GFB = 90−α Po zsumowaniu kątów w ΔGFB otrzymujemy, że ∠FGB=90 c.k.d