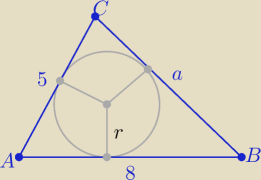
 Obwód : 2p=a+13 ⇒ a=2p−13 , p>6,5 i p∊C
P2=r2*p2
ze wzoru Herona P2=p(p−8)(p−5)(13−p)
(p−8)(p−5)(13−p)=3p
Po wymnożeniu i uporządkowaniu otrzymujemy równanie:
p3−26p2+212p−520=0 i p∊C
.......
p=10
to a=7
======
Obwód : 2p=a+13 ⇒ a=2p−13 , p>6,5 i p∊C
P2=r2*p2
ze wzoru Herona P2=p(p−8)(p−5)(13−p)
(p−8)(p−5)(13−p)=3p
Po wymnożeniu i uporządkowaniu otrzymujemy równanie:
p3−26p2+212p−520=0 i p∊C
.......
p=10
to a=7
======
| 5*8*sinα | |
=√3*p | |
| 2 |
| 5*8 | ||
2p= | *sinα | |
| √3 |
| 5*8 | ||
16<2p<26 ⇒ 16< | *sinα<26 | |
| √3 |
| 2*√3 | ||
<sinα<1 | ||
| 5 |
| √3 | ||
2p całkowite spełnia sinα= | ⇒ p=10 ⇒a=7 | |
| 2 |