5 mar 22:48
a7: można to zadanie zrobić prostszym sposobem
a mianowicie mamy siedem miejsc i liczby 1 2 3 4 5 6 7 8 9 0
na pierwszym miejscu ustawiamy jedną z liczb 1 3 5 7 9 czyli jedną z pięciu
na drugim miejscu jedną z czterech pozostałych nieparzystych czyli jedną z czterech (gdyż mają
się nie powtarzać)
na trzecim jedną z trzech pozostałych nieparzystych czyli jedną z trzech
następnie na czwartym miejscu jedną z pięciu parzystych 0 2 4 6 8
na piątym jedną z czterech pozostałych czyli jedną z czterech
na szóstych jedną z trzech pozostałych czyli jedna z trzech
na siódmym jedną z dwóch pozostałych
5*4*3*5*4*3*2=7200
5 mar 22:57
Saizou :
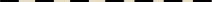
Do takich zadań podchodź "sytuacyjnie", czyli co musisz zrobić.
Każda kreska symbolizuje miejsce w systemie dziesiętnym (jedności, dziesiątki itd.)
Wiemy z zadania, że
0) cyfry się nie powtarzają
1) na pierwszych 3 miejscach mają być cyfyr nieparzyste
2) na kolejnych 4 miejscach cyfry parzyste
cyfry nieparzyste to {1, 3, 5, 7, 9}, mamy ich 5
cyfry parzyste to {0, 2, 4, 6, 8}, mamy ich 5
• na pierwszym miejscu mamy 5 możliwości (5 liczb nieaprzystych)
• na drugim 4 możliwości (bo nie może być ta sama cyfra co na pierwszym, bo się one nie mogą
powtórzyć)
• na trzecim 3 możliwości
• na czwartym 5 opcji (bo tutaj już mają być parzyste)
• na piątym 4
• na szóstym 3
• na siódmym 2
Korzystamy teraz z reguły mnożenia, czyli wszystko mnożymy
5*4*3*
5*4*3*2=60*120=7200
5 mar 22:59
salamandra: No to prawie dobrze kminiłem tylko ja napisałem
5*4*3*5*5*5*5
dzięki
5 mar 23:01
salamandra: Właśnie tym sposobem co Saizou mi napisałeś najbardziej mi przypadł i tym W MIARĘ rozumiem,
reszta to czarna magia na razie
5 mar 23:01
Saizou :
Na stronie masz taki sposób myślenia.
• na 3 miejsca muszę postawić liczbę nieparzystą i nie mogą się one powtarzać,
czyli będą to ciągi, gdzie wyrazy się nie powtarzają. Są one ze zbioru cyfr nieparzystych
(jest 5 takich cyfr).
Jest to wariacja 3−elementowa zbioru 5−elementowego
• analogicznie ta część

5 mar 23:05
salamandra: No tak, ale skąd na przykład wiadomo, że na przykład na czwartym miejscu też nie zostanie
wzięta nieparzysta? skąd "to" wie, że ma brać z parzystych, a nie dalej z nieparzystych?
5 mar 23:09
Saizou : Z treści zadania

Masz napisane 3 pierwsze to nieparzyste, kolejne to parzyste
5 mar 23:13
salamandra: No tak, ale chyba zadaje tak durne pytanie, że nawet go nie rozumiesz

spróbuję tak pokazać
pierwszą na 5 sposobów− no to dlaczego tu nie moze być 2? ja wiem, że z treści zadania, ale mam
zbiór {0−9} i jaką mam pewność, że rozwiązanie mi "nie wpisze" tej dwójki jako pierwszej?
5 mar 23:16
a7: bo rozwiązanie Ci "wpisuje" ilość możliwości i nie patrzy jakie tam się kryją pod nimi cyfry
5 mar 23:18
Saizou :
Bo bierzesz pierwszą cyfrę ze zbioru cyfr nieparzystych, a w nim nie ma cyfry 2
5 mar 23:18
a7: zobacz to na prostym przykładzie np. 0 1 2 3
liczba dwucyfrowa −pierwsza liczba nieparzysta druga parzysta bez powtarzania się cyfr
10 12 30 32 czyli cztery możliwe liczby
metodą "wymnażania możliwości"
2*2=4
5 mar 23:21
a7: liczba trzycyfrowa (z cyfr 0 1 2 3) pierwsza i trzecia cyfra nieparzysta i nie powtarzająca się
a w środku parzysta
103 123 301 321 (cztery takie liczby)
2*2*1=4
5 mar 23:24
salamandra: Magia.... przepraszam planimetrio i stereometrio
5 mar 23:24
salamandra: Można to by było inaczej zinterpretować to zadanie? Może to by mi pomogło, powiedzcie czy to
poprawnie:
Ile jest możliwości 7 cyfrowych liczb ze zbioru załóżmy (1,2,3,4,5) jeśli pierwsze trzy nie
mogą się powtórzyć, czwarta moze, a piąta szósta i siódma mogą być takie jak pierwsza, druga i
trzecia, ale miedzy sobą musza się różnic, i nie mogą być takie jak czwarta. Dobra nieważne,
już sam się w tym zagmatwalem, myślałem ze latwiej można jakoś zinterpretować, ale już wyśle
jak tyle napisałem
5 mar 23:40
wredulus_pospolitus:
No to świeże spojrzenie na zadanie.
7−cyfrowa liczba, cyfry się nie powtarzają (czyli losujemy bez zwracania

), trzy pierwsze
cyfry są nieparzyste, pozostałe parzyste
1) cyfry nieparzyste −−− 1, 3, 5, 7, 9
z tych pięciu cyfr wybieramy cyfry które będą na pierwszych trzech miejscach na:
5*4*3 sposobów (pierwsza cyfra na 5 sposobów, druga na 4, trzecia na 3)
2) cyfry parzyste −−− 0, 2, 4, 6, 8
z tych pięciu cyfra wybieramy cyfry które będą stać na czterech ostatnich miejscach. Wybieramy
je na:
5*4*3*2 sposobów
W efekcie otrzymujemy: 5*4*3*5*4*3*2 = ....
5 mar 23:51
a7: początek by się zgodził , bo byłoby 5*4*3*.... ale co znaczy, że czwarta może? może się
powtórzyć z pierwszą, drugą, trzecią? to wtedy
5*4*3*5*4*3*2=7200 no tak zgadza się, czyli zakumałeś 100%
5 mar 23:51
a7: 
5 mar 23:52
wredulus_pospolitus:
Zacznijmy od tego że zadanie napisane o 23:40 wcale takie proste nie jest i trzeba tutaj parę
różnych przypadków brać pod uwagę.
To na pewno nie jest zadanie na pierwszą lekcję prawdopodobieństwa/kombinatoryki. Więc
Salamandra − odpuść sobie takie zadanie.
5 mar 23:54
salamandra: Ok, może jutro mi się więcej rozjaśni, dzięki Wam za dziś
5 mar 23:59
a7: Wredulusie jakież to szczególne przypadki trzeba brać pod uwagę? wymień choć jeden, bo nie
rozumiem
6 mar 00:09
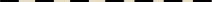 Do takich zadań podchodź "sytuacyjnie", czyli co musisz zrobić.
Każda kreska symbolizuje miejsce w systemie dziesiętnym (jedności, dziesiątki itd.)
Wiemy z zadania, że
0) cyfry się nie powtarzają
1) na pierwszych 3 miejscach mają być cyfyr nieparzyste
2) na kolejnych 4 miejscach cyfry parzyste
cyfry nieparzyste to {1, 3, 5, 7, 9}, mamy ich 5
cyfry parzyste to {0, 2, 4, 6, 8}, mamy ich 5
• na pierwszym miejscu mamy 5 możliwości (5 liczb nieaprzystych)
• na drugim 4 możliwości (bo nie może być ta sama cyfra co na pierwszym, bo się one nie mogą
powtórzyć)
• na trzecim 3 możliwości
• na czwartym 5 opcji (bo tutaj już mają być parzyste)
• na piątym 4
• na szóstym 3
• na siódmym 2
Korzystamy teraz z reguły mnożenia, czyli wszystko mnożymy
5*4*3*5*4*3*2=60*120=7200
Do takich zadań podchodź "sytuacyjnie", czyli co musisz zrobić.
Każda kreska symbolizuje miejsce w systemie dziesiętnym (jedności, dziesiątki itd.)
Wiemy z zadania, że
0) cyfry się nie powtarzają
1) na pierwszych 3 miejscach mają być cyfyr nieparzyste
2) na kolejnych 4 miejscach cyfry parzyste
cyfry nieparzyste to {1, 3, 5, 7, 9}, mamy ich 5
cyfry parzyste to {0, 2, 4, 6, 8}, mamy ich 5
• na pierwszym miejscu mamy 5 możliwości (5 liczb nieaprzystych)
• na drugim 4 możliwości (bo nie może być ta sama cyfra co na pierwszym, bo się one nie mogą
powtórzyć)
• na trzecim 3 możliwości
• na czwartym 5 opcji (bo tutaj już mają być parzyste)
• na piątym 4
• na szóstym 3
• na siódmym 2
Korzystamy teraz z reguły mnożenia, czyli wszystko mnożymy
5*4*3*5*4*3*2=60*120=7200

 Masz napisane 3 pierwsze to nieparzyste, kolejne to parzyste
Masz napisane 3 pierwsze to nieparzyste, kolejne to parzyste
 spróbuję tak pokazać
pierwszą na 5 sposobów− no to dlaczego tu nie moze być 2? ja wiem, że z treści zadania, ale mam
zbiór {0−9} i jaką mam pewność, że rozwiązanie mi "nie wpisze" tej dwójki jako pierwszej?
spróbuję tak pokazać
pierwszą na 5 sposobów− no to dlaczego tu nie moze być 2? ja wiem, że z treści zadania, ale mam
zbiór {0−9} i jaką mam pewność, że rozwiązanie mi "nie wpisze" tej dwójki jako pierwszej?
 ), trzy pierwsze
cyfry są nieparzyste, pozostałe parzyste
1) cyfry nieparzyste −−− 1, 3, 5, 7, 9
z tych pięciu cyfr wybieramy cyfry które będą na pierwszych trzech miejscach na:
5*4*3 sposobów (pierwsza cyfra na 5 sposobów, druga na 4, trzecia na 3)
2) cyfry parzyste −−− 0, 2, 4, 6, 8
z tych pięciu cyfra wybieramy cyfry które będą stać na czterech ostatnich miejscach. Wybieramy
je na:
5*4*3*2 sposobów
W efekcie otrzymujemy: 5*4*3*5*4*3*2 = ....
), trzy pierwsze
cyfry są nieparzyste, pozostałe parzyste
1) cyfry nieparzyste −−− 1, 3, 5, 7, 9
z tych pięciu cyfr wybieramy cyfry które będą na pierwszych trzech miejscach na:
5*4*3 sposobów (pierwsza cyfra na 5 sposobów, druga na 4, trzecia na 3)
2) cyfry parzyste −−− 0, 2, 4, 6, 8
z tych pięciu cyfra wybieramy cyfry które będą stać na czterech ostatnich miejscach. Wybieramy
je na:
5*4*3*2 sposobów
W efekcie otrzymujemy: 5*4*3*5*4*3*2 = ....
