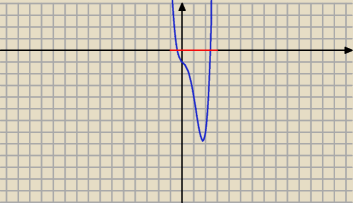
 f(−1) = 2 + 5 + 1 + 1 − 1 = 8 > 0
f (1) = 2 − 5 + 1 −1 − 1 = − 4 < 0
f ma miejsce zerowe w ( −1, 1)
f(2) = 32 − 40 + 4 − 2 − 1 = −7 < 0
f(3) = 162 − 135 + 9 − 3 − 1 = 32 > 0
f ma miejsce zerowe w( 2, 3)
f(−1) = 2 + 5 + 1 + 1 − 1 = 8 > 0
f (1) = 2 − 5 + 1 −1 − 1 = − 4 < 0
f ma miejsce zerowe w ( −1, 1)
f(2) = 32 − 40 + 4 − 2 − 1 = −7 < 0
f(3) = 162 − 135 + 9 − 3 − 1 = 32 > 0
f ma miejsce zerowe w( 2, 3)
| 5 | 59 | 5 | 117 | 5 | 4403 | |||||||
2(x− | )4− | (x− | )2− | (x− | )− | =0 | ||||||
| 8 | 16 | 8 | 32 | 8 | 2048 |
| 5 | 59 | 5 | 117 | 5 | 4403 | |||||||
(x− | )4− | (x− | )2− | (x− | )− | =0 | ||||||
| 8 | 32 | 8 | 64 | 8 | 4096 |
| 59 | 117 | 4403 | ||||
y4− | y2− | y− | =0 | |||
| 32 | 64 | 4096 |
| 59 | 117 | 4403 | ||||
(y2−py+q)(y2+py+r)=y4− | y2− | y− | ||||
| 32 | 64 | 4096 |
| 59 | 117 | 4403 | ||||
y4+py3+ry2−py3−p2y2−pry+qy2+pqy+qr=y4− | y2− | y− | ||||
| 32 | 64 | 4096 |
| 59 | 117 | 4403 | ||||
y4+(q+r−p2)y2+(pq−pr)y+qr=y4− | y2− | y− | ||||
| 32 | 64 | 4096 |
| 59 | 117 | 4403 | ||||
y4+(q+r−p2)y2+p(q−r)y+qr=y4− | y2− | y− | ||||
| 32 | 64 | 4096 |
| 59 | ||
q+r−p2=− | ||
| 32 |
| 117 | ||
p(q−r)=− | ||
| 64 |
| 4403 | ||
qr=− | ||
| 4096 |
| 59 | ||
q+r=− | +p2 | |
| 32 |
| 117 | 1 | ||
q−r=− | |||
| 64 | p |
| 4403 | ||
4qr=− | ||
| 1024 |
| 59 | 117 | 1 | 59 | 117 | 1 | 4403 | ||||||
(− | +p2− | )(− | +p2+ | )=− | ||||||||
| 32 | 64 | p | 32 | 64 | p | 1024 |
| 3481 | 59 | 13689 | 1 | 4403 | |||||
( | − | p2+p4− | )=− | ||||||
| 1024 | 16 | 4096 | p2 | 1024 |
| 3481 | 59 | 13689 | 4403 | ||||
p2− | p4+p6− | + | p2=0 | ||||
| 1024 | 16 | 4096 | 1024 |
| 59 | 1971 | 13689 | ||||
p6− | p4+ | p2− | =0 | |||
| 16 | 256 | 4096 |
| z | ||
p2= | ||
| 16 |
| 1 | 59 | 1971 | 13689 | ||||
z3− | z2+ | z− | =0 | ||||
| 4096 | 4096 | 4096 | 4096 |
| 9 | ||
p2= | ||
| 16 |
| 3 | ||
p= | ||
| 4 |
| 59 | ||
q+r=− | +p2 | |
| 32 |
| 117 | 1 | ||
q−r=− | |||
| 64 | p |
| 4403 | ||
4qr=− | ||
| 1024 |
| 59 | 117 | 1 | |||
2q=− | +p2− | ||||
| 32 | 64 | p |
| 59 | 117 | 1 | |||
2r=− | +p2+ | ||||
| 32 | 64 | p |
| 4403 | ||
4qr=− | ||
| 1024 |
| 3 | ||
p= | ||
| 4 |
| 59 | 9 | 117 | 4 | ||||
2q=− | + | − | |||||
| 32 | 16 | 64 | 3 |
| 59 | 9 | 117 | 4 | ||||
2r=− | + | + | |||||
| 32 | 16 | 64 | 3 |
| 3 | ||
p= | ||
| 4 |
| 59 | 9 | 39 | ||||
2q=− | + | − | ||||
| 32 | 16 | 16 |
| 59 | 9 | 39 | ||||
2r=− | + | + | ||||
| 32 | 16 | 16 |
| 3 | ||
p= | ||
| 4 |
| 59 | 30 | |||
2q=− | − | |||
| 32 | 16 |
| 59 | ||
2r=− | +3 | |
| 32 |
| 3 | ||
p= | ||
| 4 |
| 119 | ||
2q=− | ||
| 32 |
| 37 | ||
2r= | ||
| 32 |
| 3 | ||
p= | ||
| 4 |
| 119 | ||
q=− | ||
| 64 |
| 37 | ||
r= | ||
| 64 |
| 59 | 117 | 4403 | ||||
(y2−py+q)(y2+py+r)=y4− | y2− | y− | ||||
| 32 | 64 | 4096 |
| 3 | 119 | 3 | 37 | 59 | 117 | 4403 | ||||||||
(y2− | y− | )(y2+ | y+ | )=y4− | y2− | y− | ||||||||
| 4 | 64 | 4 | 64 | 32 | 64 | 4096 |
| 5 | 3 | 5 | 119 | |||||
2((x− | )2− | (x− | − | )) | ||||
| 8 | 4 | 8 | 64 |
| 5 | 3 | 5 | 37 | |||||
((x− | )2+ | (x− | + | ))=2x4 −5x3 +x2 −x−1 | ||||
| 8 | 4 | 8 | 64 |
| 5 | 25 | 3 | 15 | 119 | ||||||
2(x2− | x+ | − | x+ | − | ) | |||||
| 4 | 64 | 4 | 32 | 64 |
| 5 | 25 | 3 | 15 | 37 | ||||||
(x2− | x+ | + | x− | + | )=2x4 −5x3 +x2 −x−1 | |||||
| 4 | 64 | 4 | 32 | 64 |
| 1 | 1 | |||
2(x2−2x−1)(x2− | x+ | )=2x4 −5x3 +x2 −x−1 | ||
| 2 | 2 |
| 2−2√2 | ||
x1= | ||
| 2 |
| 2+2√2 | ||
x2= | ||
| 2 |