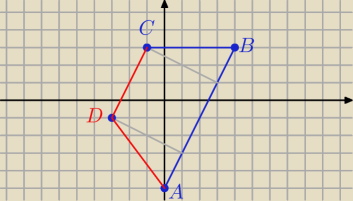
Wektory, geomeria analityczna Chorus: Punkty A=(0, −5) B=(4, 3) i C=(−1, 3) sa wierzcholkami trapezu rownoramiennego ABCD o podstawach AB i CD. Wyznacz wspolrzedne wierzchołka D. Obliczyłem: a)równanie prostej AB b) równanie prostej _I do AB c) punkt przecięcia AB i prostej prostopadłej Nie jestem pewien co dalej robić. Liczyć współrzędne wektorów EB i CD?

janek191:

Chorus: *powinno być b) równanie prostej prostopadłej do AB

wredulus_pospolitus: Janek −−− to nie jest jedyna możliwość. To może być też równoległobok

janek191:

wredulus_pospolitus: Polecam zrobić to w ten sposób: a) równanie prostej zawierającej AB b) równanie prostej równoległej do (a), przechodzącej przez punkt C c) wyznaczenie długości odcinka BC d) wyznaczenie wzoru okręgu o promieniu |BC| i środku w A e) punkt przecięcia się prostej (b) z okręgiem (d) daje nam dwie możliwe lokalizacje punktu D. Wypisujesz oba.

Chorus: dzięki wielkie

Chorus: jeszcze małe pytanie. Co gdybym miał w zamyśle zadania że nie jest równoległobokiem? czy mogę wtedy skorzystać z współrzędnych wektorów BC?

wredulus_pospolitus: I co Ci to da Właśnie, gdyby to był równoległobok, wtedy mógłbyś zrobić wykorzystując wektory: BA + BC