Arkusz Patryk: Cześć, Zacząłem robić sobie maturę próbna ze strony zadania.info ale średnio z odpowiedziami. Czy mógłby ktoś sprawdzić czy poprawnie zrobiłem te zadania do którym podam odpowiedzi? Nie będę wszystkich odpowiedzi pisał na razie bo nie mam czasu ale może jutro napisze następne a tymczasem: zad 1: odp. C (musi być tam funkcja liniowa i do tego malejąca) zad 2: odp. A zad 3: odp A zad 4: odp C bo w mianowniku będzie miejsce zerowe zad 5: odp. C −> to w sumie zrobiłem w taki sposób że naszkicowałem sytuacje na rysunku i najpierw sprawdziłem które punkty należą do odcinka AC a później sprawdzałem graficznie który trapez wygląda na 5/9 pola trójkąta zad 6: dopiero niedawno zacząłem prawdopodobieństwo w szkole, ale wydaje mi się że dobrze zrobiłem. Zrobiłem za pomoca drzewka, napisałem przy gałęziach prawdop. dla danych gałęzi i wyszło mi :

	2		11		22
P(A) =		*		=
	3		17		51

zad 7: nie będę przepisywał wszystkich obliczeń bo sporo tego ale pod koniec wyszło mi:

	3   1   n2(3− + )   n   n2		3n2		3
lim n→+∞ =		=		=
	64   n*3√n3(343+ )   n2		7n2		7

I ostatnie zadanie na dzisiaj, zad 8: tutaj zrobiłem to tak, że oznaczyłem sobie boki kolejno wgł. polecenia a, a+r, a+2r i a+3r i napisałem, że ponieważ suma przeciwległych boków czworokąta jest równa więc dwusieczne przecinają się w jednym punkcie.(Można w niego wpisać okrąg). Na razie to tyle

Patryk: Arkusz: https://zadania.info/d1775/75844

Saizou : Wykup sobie abonament to masz tam rozwiązania. Zresztą możesz kupić na 20 min i pobrać więcej arkuszy z rozwiązaniami

Patryk: Kurcze, ciekawe tam ceny mają, 20 min... dobrze, że nie na 27min i 30 s.

Saizou : Już się nie czepiaj, jakoś muszą utrzymać serwer

Patryk: To resztę zadań jakoś ogarnę a te które już zdążyłem wrzucić tutaj na forum mógłby na nie ktoś zerknąć?

a@b: zad.12 4pkt śmiechu warte to jest zadanie dla podstawówki odp: n=37

wredulus_pospolitus: 1) ok 2) ok 3) ok 4) ok 5) nie chce mi się tego rysować 6) ok 7) ok

Patryk: Ok, dzięki wielkie! Fakt to 12 zadanie trochę za proste, tylko pod wzór podstawić

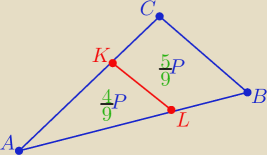
a@b: Zad 5 Z podobieństwa trójkątów ABC i AKL

PΔ(AKL)		4		2
	= k2 ⇒ k2=		⇒ k=
P(Δ(ABC)		9		3

to → → AK=(2/3)AC [x+1, y+1]=[4,6] ⇒ x=3 i y= 5 K(3,5) ======= Co można sprawdzić w układzie współrzędnych ( nawet bez obliczeń) bo to zadanie testowe i podać odp

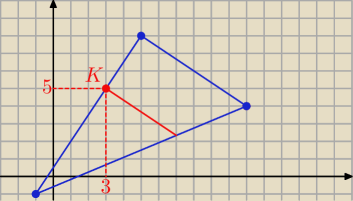
a@b: Inne nie pasują

Patryk: To może, wrzucę jutro resztę pojedynczych odpowiedzi do tych zadań bo szkoda mi troche kasy jednorazowo kupowac ten pakiet żeby tylko pobrać odpowiedzi do jednego arkusza. Bo do innych zadań odpowiedzi są w necie. Wrzuce dzisiaj jeszcze tylko jedno zadanie, które zrobiłem, zad 11: już bez pisania obliczeń bo dużo potęg i za duzo pisania P₁:

	7
x1 + x2 = 3/div>
	2

	5
x1*x2 = −23*3/div>
	2

	3
P1 = −
	8

P₂:

	15
x1+x2 = 3/div>
	2

	11
x1x2 = −26*3/div>
	2

	9
P2 = −
	64

	P2		3
q =		=		należy do (−1;1)
	P1		8

	P1		3
Sn =		= −
	1−q		5

Po div jest ułamek który jest w potędze, nie potrafiłem tego odpowiednio napisać żeby poprawnie się wyświetlało

a@b:

1		1		−b
	+		=
x1		x2		c

	−b		92n		3
to pn=		⇒pn=−		⇒pn= −(		)n
	c		63n		8

	3		3
p1=−		, q=		, |q|<1 −−− ciąg geometryczny zbieżny
	8		8

	3   −   8		−3
zatem S=		=
	3   1−   8		8−3

	3
S= −
	5

=======

Patryk: Czyli kolejne dobrze , dzięki. Może w maju nie będzie tak źle Rozwiąże reszte jutro gdy wróce ze szkoły

a@b:

Patryk: Następna partia, Zad 10 n⁴ − 17n² + 7 = 0 p = n², p>0 p² − 17p + 7 = 0 Δ = 216, √Δ = 3√29

	17−3√29		17+3√29
(p−		)(p−		)
	2		2

Skoro liczba nie dzieli się przez 3 to: n = 3k+1 lub 3k+2, k∊C p = (3k+1)² lub p = (3k+2)² Dla 3k+1:

	17−3√29		17+3√29
((3k+1)2 −		)((3k+1)2 −		) =
	2		2

	18k2+12k−15+3√29		18k2+12k−15−3√29
(		)(		) = 9(......)(.......) −−−−> czyli dzieli
	2		2

się na 9 I to samo robię "dla 3k+2", będzie poprawnie?

wredulus_pospolitus: tragedia szerze mówiąc. Zauważ, że: jeżeli n = 3k+1 to n² = 9k² + 6k + 1 = 3j + 1 <−−− daje resztę 1 jeżeli n = 3k + 2 to n² = 9k² + 12k + 4 = 3l + 1 <−−− daje resztę 1 więc skoro n = 3k+1 lub n =3k+2 to n² = 3j + 1 oraz n⁴ = 3m + 1 n⁴ − 17n² + 7 = n⁴ − 17n² + 6 + 1 = 3m+1 − 17*(3j+1) + 6 + 1 = = 3(m − 17j) + 1 − 17 + 6 + 1 = 3(m−17j) − 9 = 3(m − 17j − 3) c.n.w.

wredulus_pospolitus: a jak już chcesz rozpisywać wielomian, to np. w taki sposób: n⁴ − 17n² + 7 = n⁴ − 10n² − 7n² + 49 + 7 − 49 = = (n²−10)(n² − 7) − 42 = (n²−10)(n² − 7) − 7*6 = (*) n = 3k + 1 lub n = 3k+2 ... więc n² = 3l + 1 (*) = (3l + 1 − 10)(3l + 1 − 7) − 7*6 = (3l − 9)(3l − 6) − 7*6 = ... dokończ

Patryk: No na to bym nie wpadł A to moje nie przejdzie w jakimś stopniu?

Patryk: Dobra, kapuję, a przy tym n² = 3l+1 zamiast podstawiać nową zmienną "l" mógłbym po prostu spotęgować: (3k+1)²?

wredulus_pospolitus: możesz spotęgować

wredulus_pospolitus: istotne jest by zauważyć, że dla n = 3k+1 n² daje resztę 1 n = 3k+2 n² także daje resztę 1

wredulus_pospolitus: A to co robiłeś może i by przeszło jakbyś zrobił do końca ... ale: 1) za dużo roboty z tym 2) w tej postaci jak zostawiłeś szczerze mówiąc nie widzę podzielności przez 3

Patryk: A mógłbyś jeszcze przedstawić swój tok myślenia przy rozkładzie tego wielomianu tak żeby doprowadzić do sytuacji gdzie można użyć wzoru skróconego mnożenia. Przydała by mi się taka informacja/lekcja biorąc pod uwagę, że często się przydaje taki rozkład przy zadaniach z dowodzeń a u mnie zadań z dowodzeń nawet się "się nie rusza"

wredulus_pospolitus: wiemy że n² daje resztę 1 ... więc chce rozłożyć wielomian na: (n² − a)(n² − b) + c gdzie zachodzi przynajmniej jedno z poniższych: a daje resztę 1 b daje resztę 1 wtedy (n²−a)(n²−b) będzie podzielne przez 3 (daje resztę 0) więc można go dowolnie rozłożyć byleby 'a' było postaci 3p + 1, ja wybrałem a = 3*3 + 1 = 10

Patryk: Dzięki! Musze trochę porobić zadań tego typu żeby załapać o co chodzi. Zadania 12 nie będe pisał bo za proste Zad. 13

	x
sin2x = cos2x + cos
	π

	x
cos2x + cos		= 0
	π

	5		3
2cos(		x)cos(		)x = 0
	4		4

	5
1) cos(		)x = 0
	4

5		π
	x =		+ kπ
4		2

	2π+4kπ
x =
	5

	3
2)cos(		)x = 0
	4

3		π
	x =		+ kπ
4		2

	2π+4kπ
x =
	3

Dla <−2π ;2π> Z 1) mam rozwiązania dla k={−3, −2, −1, 0, 1, 2} Z 2) mam dla k={−2, −1, 1, 0} Już nie pisałem konkretnie jakie x−y bo za dużo ułamków