prawdopodobieństwo salamandra: Żeby tamtego wątku nie zaśmiecać już Zad. Ze zbioru cyfr {0,1,2,3,4} losujemy kolejno dwie. Pierwszą z nich zapisujemy jako cyfrę dziesiątek, drugą jako cyfrę jedności. Oblicz prawdopobieństwo zdarzenia A, że będzie to liczba jednocyfrowa. Liczbę dziesiątek mogę wybrac na 4 sposoby, a liczbę jedności na 5, więc wszystkich liczb (wariacji/kombinacji/permutacji?) będzie 20.

	4		1
Jednocyfrowe to tylko 1,2,3,4, więc prawdopodobieństwo to		=		, o to chodzi?
	20		5

wredulus_pospolitus: niee ... źle Twoja Ω NIE ZAWIERA w sobie liczb jednocyfrowych Druga sprawa −−− czy losowanie jest bez zwracania czy ze zwracaniem (nie napisałeś tego)

salamandra: Przepisałem całą treść zadania

wredulus_pospolitus: Więc rozwiążmy, to dwóch możliwościach: 1) Bez zwracania. #Ω = 5*4 (tak ... 0 może być jako pierwsze wylosowane) #A = 1*4 (jako pierwsze 0, później dowolna z pozostałych)

	1*4		1
P(A) =		=
	5*4		5

2) Z zwracaniem. #Ω = 5*5 #A = 1*5

	5*5		1
P(A) =		=
	1*5		5

Jak widzisz ... w obu przypadkach wyszedł taki sam wynik (nie musi tak być). Tobie też wyszedł taki sam wynika ale ... TY źle to rozwiązywałeś, ponieważ: #Ω policzyłeś jako 4*5 czyli (na pozycji dziesiątek nie może być 0, na pozycji jedności może być dowolna, w tym także ta co na pozycji dziesiątek) Więc nie dość, że w Ω masz TYLKO I WYŁĄCZNIE liczby dwucyfrowe (nie ma np. 01) to w dodatku tutaj losowanie jest ze zwracaniem #A policzyłeś natomiast BEZ ZWRACANIA (bo nie ma układu 00 czyli liczby 0), a także (co bardziej haniebnym błędem jest) zdarzenie A nie zawiera się w Ω

salamandra: ale jak to zero moze byc jako pierwsze wylosowane? jak to wtedy rozpatrujemy?

wredulus_pospolitus: zauważ, że w zadaniu chodzi oto żeby policzyć prawdopodobieństwo że z otrzymanych cyfr ułożyć liczbę JEDNOcyfrową

salamandra: czyli 04 traktujemy jako 4? czyli jednocyfrową? bo nie rozumiem

wredulus_pospolitus: Dokładnie tak.

salamandra: aha, no to to zmienia postać rzeczy

salamandra: i 00 to też jest ta jednocyfrowa liczba? bo probowalem to sam zrobic tak jak Ty i zawahałem się przy "ze zwracaniem" i z 1*5

wredulus_pospolitus: tak ... w końcu 00 oczytujemy po prostu jako liczbę 0 (jednocyfrowa liczba)

salamandra: Mam zadanie: Z cyfr 2 i 3 tworzymy liczby trzycyfrowe. Sporządź graf doświadczenia losowego i a) wypisz wszystkie zdarzenia elementarne przestrzeni Ω. i tutaj mogę w ten sposób, czy znów będzie źle pierwszą drugą i trzecią cyfrę mogę wybrać na dwa sposoby więc 2*2*2=8 Jest 8 takich cyfr. b) oblicz prawdopobieństwo 1. zdarzenia A, że utworzona liczba jest parzysta. 2. zdarzenia B, że utworzona liczba jest podzielna przez 3. 1.pierwsza na dwa sposoby, druga też na dwa, i trzecia na jeden sposób (musi mieć 2 na końcu), więc 2*2*1=4

	4		1
więc P(A)=		=
	8		2

2. liczba jest podzielna przez 3, jeżeli suma jej cyfr jest równa 3, i tutaj nie mam pomysłu więc wypiszę

	2		1
222,333, więc P(B)		=		?
	8		4

wredulus_pospolitus: a) Jest 8 taki liczb i gdzie ten graf

wredulus_pospolitus: b) 1. ok 2. ok

salamandra: Nie wiem o co chodzi z tym grafem, po co to komu

wredulus_pospolitus: co do (b) 2. tutaj podchodzimy do tego tak: dzielimy cyfry jakie mamy dostępne na podgrupy: te które mają resztę 0 przy dzieleniu przez 3, te które mają resztę 1 przy dzieleniu przez 3, te które mają resztę 2 przy dzieleniu przez 3 Później zastanawiamy się (bo to zależy od treści zadania) jakie kombinacje z tych podgrup wchodzą w rachubę, gdybyśmy mieli cyfrę 1 także, to byśmy mogli utworzyć: 1. 3 cyfry o reszcie 0 2. 3 cyfry o reszcie 1 3. 3 cyfry o reszcie 2 4. cyfra o reszcie 0, cyfra o reszcie 1, cyfra o reszcie 2

wredulus_pospolitus: 'drzewko' narysuj

salamandra: nie rozumiem za bardzo, (przynajmniej na razie), tego drzewka,

wredulus_pospolitus:

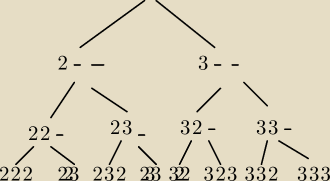
	1
i przy każdej gałęzi piszesz prawdopodobieństwo ... w każdej będzie
	2

Jerzy: Skąd masz to zadanie ?

salamandra:

	1
czyli szansa na wylosowanie 2−− lub 3−− to
	2

	1		1
niżej to		, a na samym dole to		?
	4		8

salamandra: Z podręcznika Podkowa Jerzy

Jerzy: Pytam,bo rysowanie drzewka w tym zadaniu jest absurdem.

wredulus_pospolitus:

	1
nie ... poziom niżej też cały czas
	2

bo to czytasz jako ... masz 2 _{− −} jaka jest szansa uzyskania z tego 22 ₋ oczywiście

	1
	2

	1
więc przy każdej gałęzi będziesz mieć
	2

natomiast drzewko działa tak, że później zaznaczasz CAŁĄ gałąź sprzyjającą i wtedy wymnażasz wszystkie napotkane prawdopodobieństwa + wymnożone prawdopodobieństwa z innej sprzyjającej gałęzi

	1		1		1		1		1		1
więc będzie		*		*		+		*		*		<−−− co reprezentuje gałąź
	2		2		2		2		2		2

idącą do 222 + gałąź idącą do 333

salamandra:

	1
No tak, ale pytałem jakby z całej puli jaka jest szansa żeby uzyskać 22−, wtedy		tak?
	4

salamandra:

	1
to że z puli 22−, uzyskanie 223 lub 222 jest
	2

salamandra: to wiem

wredulus_pospolitus:

	1		1		1
tak ... uzyskanie 2 2 − jest z prawdopodobieństwem		*		=
	2		2		4

salamandra: A w tym: Rzucono trzy razy symetryczną monetą. Oblicz prawdopodobieństwo zdarzenia A, że otrzymano trzy orły, oraz zdarzenia B, że otrzymano dwa orły Wiem, że to można sobie rozpisać ale już chcę sobie liczyć do trudniejszych przykładów sposób, więc− wszystkich możliwości jest 8., bo 2*2*2=8 żeby był orzeł to w pierwszym rzucie jedna mozliwosc, w drugim jedna i w trzecim jedna czyli 1*1*1=1

	1
P(A)=
	8

dwa orły czyli w pierwszym jedna mozliwosc, w drugim jedna i w trzecim dwie, czyli 1*1*2=2

	1
P(B)=
	4

	3
no i tutaj coś mi się psuje, bo wynik powinein być		, wiem że wypisując sobie łatwo bym
	8

to dostrzegł, ale jak to algebraicznie zrobić?

wredulus_pospolitus: (a) ok (b) ... dlaczego tak liczysz ... słownie wyjaśnij nam dlaczego robisz 1*1*2 później Ci napiszę (słownie) jak powinno się mnożyć

salamandra: no 1*1*2, no bo pierwszą możemy wybrać na jeden sposób, drugą też (no bo tylko orzeł), a drugą na dwa (orzeł lub reszka), ale w sumie raczej tak myślałem, bo teraz to widzę, że to się kupy nie trzyma, bo w tym momencie mogę również wylosować (reszka, reszka, reszka), czyż nie?

salamandra: Chyba po prostu za bardzo kombinuję prawda?

wredulus_pospolitus: to co policzyłeś odpowiada treści: prawdopodobieństwo że W DWÓCH PIERWSZYCH rzutach wypadną orły (a w trzecim 'cokolwiek' − przyp. red.) Ale tak jak napisałem, to się kupy nie trzyma. Ale nie R,R,R nie może być wylosowane w takim zdarzeniu co napisałeś.

wredulus_pospolitus: (b) masz wylosować (dokładnie) dwa orły. Więc chodzi o losowanie: Dwa orły i jedna reszka. ile jest takich układów: 1*1*1 (czyli konkretny układ: O,O,R) * 'permutacja' tegoż układu na ile sposobów można permutować? Na 3 sposoby O,O,R ; O,R,O ; R,O,O I stąd masz 1*1*1*3 = 3 Inny sposób podejścia do zagadnienia. Masz wylosować raz reszkę i dwa razy orła, w trzech rzutach. Krok 1: wybieramy sobie w którym rzucie wypadnie reszka. Wybieramy to na 3 sposoby (pierwszy, drugi lub trzeci rzut) Krok 2: w pozostałych rzutach MUSI wypaść orzeł. Podsumowanie: 3*1*1 = 3

salamandra: "ile jest takich układów: 1*1*1 (czyli konkretny układ: O,O,R) * 'permutacja' tegoż układu na ile sposobów można permutować? Na 3 sposoby O,O,R ; O,R,O ; R,O,O I stąd masz 1*1*1*3 = 3" to do mnie trafia!

salamandra: chociaż nie, nie rozumiem, bo permutowac na trzy sposoby, to znaczy ustawiać w różnej kolejności, to dla zbioru trzyelementowego nie będzie to 3! ? np. {1,2,3}, można ustawić na sześć różnych sposobów?

wredulus_pospolitus: A miałeś permutacje Z POWTÓRZENIAMI

wredulus_pospolitus: tu masz sytuację {1,1,2} <−−− na ile sposobów można permutować. gdzie 1 −− orzeł, 2 −−− reszka.

salamandra: niezbyt, mialem tylko krotkie wprowadzenie w ogole do kombinatoryki.

wredulus_pospolitus: to spróbujmy tak. mamy O₁, O₂, R <−−− to można permutować na 3! = 6 sposobów ... okey ale O₁ i O₂ to jedno i to samo ... dlatego {O₁, O₂, R} i {O₂, O₁, R} przedstawiają ten sam układ

	3!
Dlatego musimy to podzielić przez 2! .... stąd		= 3
	2!

Jerzy: Za dużo chcesz zrozumieć na raz. (O,O,R) jeśli permutujesz, to korzystasz ze wzoru 3! = 6 Dlaczego zatem dla tego układu, to wynik 3 ?

Jerzy: Już ci Bleee odpowiedział, ale musisz to rozumieć

salamandra: Nie tyle Jerzy chcę za dużo zrozumieć na raz, tylko to wszystko to praca domowa, którą muszę zrobić.... Ja wszystko wiem jak "logicznie" wytłumaczyc i sobei wypisać wszystkie mozliwości, ale wiem, że w trudniejszych zadaniach nie będę mógł tego zrobić i chcę znać mechanizm

Jerzy: Ile słów można utworzyć ze słowa MATEMATYKA ( zakładamy,że każdy ciąg liter jest słowem ) ?

salamandra: Wiem, że O1 i O2 to to samo, ale wlasnie dlaczego akurat się dzieli przez to? Tych wzorów nie umiem wpoić

wredulus_pospolitus: Zostawmy ten przykład na moment. Szybkie wprowadzenie do 'permutacji z powtórzeniami'. Ile różnych 'słów' można utworzyć z liter tworzących słowo "BATY" Odpowiedź: 4! = 24 Rozumiemy dlaczego, prawda A ile różnych 'słów' można utworzyć z liter tworzących słowo "BABY"

	4!
Odpowiedź:		= 12 ponieważ dwukrotnie mamy tę samą literę 'B'
	2!

A ile różnych 'słów' można utworzyć z liter tworzących słowo "BABA"

	4!
Odpowiedź:		= 6 ponieważ dwukrotnie mamy tę samą literę 'B' oraz dwukrotnie mamy
	2!*2!

tę samą literę 'A'

Jerzy: Nie żartuj.Zaczynasz kombinatorykę i już jesteś w rachunku prawdopodobieństwa ? Do jakiej chodzisz szkoły ?

wredulus_pospolitus: Przy słowie MATEMATYKA było by to:

10!
2!*3!*2!

czyli dzielimy przez permutację ilości liter 'M' (2 sztuki) * permutację ilości liter A (3 sztuki) * permutację ilości litery 'T' (2 sztuki).

Jerzy: @ Bleee...wyprzedzasz mnie o krok,ale chcemy do niego dotrzeć w ten sam sposób

salamandra: Nie żartuję Jerzy, wczoraj jedna lekcja o regule mnożenia, dzisiaj wprowadzenie do kombinatoryki, ten eksperyment o którym pisałem z pięcioma osobami i wybieraniu trzech, definicja i wzory permutacje, wariacje, kombinacja i tyle.

salamandra: 20:21 wredulus, rozumiem to wszystko co zrobiłeś, tylko nie wiem z czego wynika, że akurat trzeba podzielić, są jakieś dowody na te wzory?

wredulus_pospolitus: Ponieważ słowo BABY można przestawić jako B₁AB₂Y, B₂AB₁Y B₁AYB₂, B₂AYB₁, B₁YAB₂, B₂YAB₁, B₁YB₂A, B₂YB₁A, B₁B₂YA, B₂B₁YA, B₁B₂AY, B₂B₁AY, itd. (nie chce mi się wszystkich możliwości wypisywać) Jako, że B₁ i B₂ oznaczają to samo to otrzymujesz dokładnie o 2! (czyli permutacja '2' jednakowych elementów) za dużo I stąd konieczne jest wykonanie dzielenia. Ogólny wzór na permutację z powtórzeniami wygląda tak:

n!
	gdzie ni oznacza ilość występowań elementu 'i'
n1!*n2!*n3!*...*nk!

salamandra: Rozumiem, zapamiętam ten wzór i tyle, za często chcę za głęboko wejść w temat i potem się zapętlam niepotrzebnie, Krok po kroku mam nadzieję, że to ogarnę